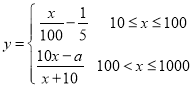题目内容
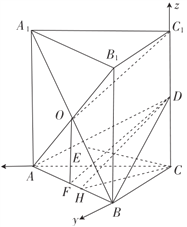
【题目】如图，在直三棱柱
中，
，
为棱
的中点，
.
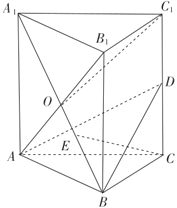
（1）证明：
平面
；
（2）设二面角
的正切值为
，
，
，求异面直线
与
所成角的余弦值.
【答案】（1）见解析（2）
【解析】试题分析：（1）取
的中点
,根据平行四边形性质得
，再根据线面平行判定定理得结论，（2）根据条件建立空间直角坐标系，设立各点坐标，根据向量数量积求向量夹角，最后根据线线角与向量夹角相等或互余关系确定结果.
试题解析：（1）证明：取的中点，连接
，
，
∵侧面
为平行四边形，∴
为
的中点，
∴
，又
，∴
，
∴四边形
为平行四边形，则.
∵
平面
，
平面，∴
平面.
（2）解：过
作
于
，连接
，
则
即为二面角
的平面角.
∵
，
，∴
.
以为原点，建立空间直角坐标系
，如图所示，则
，
，
，
，
则
，
，
.
∵
，∴
，
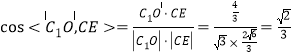∴异面直线
与
所成角的余弦值为.
名师金手指领衔课时系列答案
【题目】某大学为了调查该校学生性别与身高的关系，对该校1000名学生按照
的比例进行抽样调查，得到身高频数分布表如下：
男生身高频率分布表
男生身高 （单位：厘米） |
|
|
|
|
|
|
频数 | 7 | 10 | 19 | 18 | 4 | 2 |
女生身高频数分布表
女生身高 （单位：厘米） |
|
|
|
|
|
|
频数 | 3 | 10 | 15 | 6 | 3 | 3 |
（1）估计这1000名学生中女生的人数；
（2）估计这1000名学生中身高在
的概率；
（3）在样本中，从身高在
的女生中任取3名女生进行调查，设
表示所选3名学生中身高在
的人数，求的分布列和数学期望.（身高单位：厘米）
【题目】有一名高二学生盼望2020年进入某名牌大学学习，假设该名牌大学有以下条件之一均可录取：①2020年2月通过考试进入国家数学奥赛集训队（集训队从2019年10月省数学竞赛一等奖中选拔）：②2020年3月自主招生考试通过并且达到2020年6月高考重点分数线，③2020年6月高考达到该校录取分数线（该校录取分数线高于重点线），该学生具备参加省数学竞赛、自主招生和高考的资格且估计自己通过各种考试的概率如下表
省数学竞赛一等奖 | 自主招生通过 | 高考达重点线 | 高考达该校分数线 |
0.5 | 0.6 | 0.9 | 0.7 |
若该学生数学竞赛获省一等奖，则该学生估计进入国家集训队的概率是0.2.若进入国家集训队，则提前录取，若未被录取，则再按②、③顺序依次录取：前面已经被录取后，不得参加后面的考试或录取.（注：自主招生考试通过且高考达重点线才能录取）
（Ⅰ）求该学生参加自主招生考试的概率；
（Ⅱ）求该学生参加考试的次数
的分布列及数学期望；
（Ⅲ）求该学生被该校录取的概率.
【题目】为了了解市民对开设传统文化课的态度，教育机构随机抽取了
位市民进行了解，发现支持开展的占
，在抽取的男性市民
人中持支持态度的为
人.
（1）完成
列联表，并判断是否有
的把握认为性别与支持与否有关？
支持 | 不支持 | 合计 | |
男性 | |||
女性 | |||
合计 |
（2）为了进一步征求对开展传统文化的意见和建议，从抽取的位市民中对不支持的按照分层抽样的方法抽取
位市民，并从抽取的人中再随机选取
人进行座谈，求选取的人恰好为
男女的概率.
附：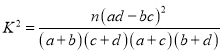
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
