题目内容
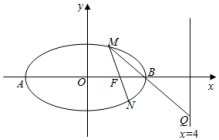
【题目】在平面直角坐标系xOy中,椭圆C的中心在坐标原点O,其右焦点为![]() ,且点
,且点![]() 在椭圆C上.
在椭圆C上.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 设椭圆的左、右顶点分别为A、B,M是椭圆上异于A,B的任意一点,直线MF交椭圆C于另一点N,直线MB交直线
设椭圆的左、右顶点分别为A、B,M是椭圆上异于A,B的任意一点,直线MF交椭圆C于另一点N,直线MB交直线![]() 于Q点,求证:A,N,Q三点在同一条直线上.
于Q点,求证:A,N,Q三点在同一条直线上.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)设椭圆的方程为![]() ,由题意可得
,由题意可得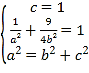 ,解方程组即可.
,解方程组即可.
(2)设![]() ,
,![]() ,直线MN的方程为
,直线MN的方程为![]() ,由方程组
,由方程组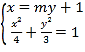 ,消去
,消去![]() 整理得
整理得![]() ,根据韦达定理求出点
,根据韦达定理求出点![]() 的坐标,根据向量即可求出
的坐标,根据向量即可求出![]() ,且向量
,且向量![]() 和
和![]() 有公共点
有公共点![]() ,即可证明.
,即可证明.
(1)不妨设椭圆的方程为![]() ,
,![]() .
.
由题意可得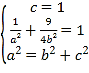 ,解得
,解得![]() ,
,![]() ,
,
故椭圆的方程![]() .
.
(1)设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
由方程组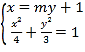 ,消去x整理得
,消去x整理得![]()
![]()
![]() ,
,![]() ,
,
![]() 直线
直线![]() 的方程可表示为
的方程可表示为![]() ,
,
将此方程与直线![]() 成立,可求得点
成立,可求得点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,![]() ,
,
![]()
![]()
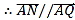 ,
,
![]() ,
,
![]() 向量
向量![]() 和
和![]() 有公共点
有公共点![]() ,
,
![]() ,
,![]() ,
,![]() 三点在同一条直线上.
三点在同一条直线上.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】下表列出了10名5至8岁儿童的体重x(单位kg)(这是容易测得的)和体积y(单位dm3)(这是难以测得的),绘制散点图发现,可用线性回归模型拟合y与x的关系:
体重x | 17.00 10.50 13.80 15.70 11.90 10.20 15.00 17.80 16.00 12.10 |
体积y | 16. 70 10.40 13.50 15.70 11.60 10.00 14.50 17.50 15.40 11.70 |
(1)求y关于x的线性回归方程![]() (系数精确到0.01);
(系数精确到0.01);
(2)某5岁儿童的体重为13.00kg,估测此儿童的体积.
附注:参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,137×14=1918.00.
,137×14=1918.00.
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: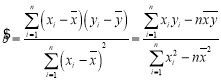 ,
,![]() .
.