题目内容
【题目】如图,扇形AOB是一个观光区的平面示意图,其中圆心角∠AOB为![]() ,半径OA为1 km.为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由弧AC、线段CD及线段DB组成,其中D在线段OB上,且CD∥AO.设∠AOC=θ.
,半径OA为1 km.为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由弧AC、线段CD及线段DB组成,其中D在线段OB上,且CD∥AO.设∠AOC=θ.
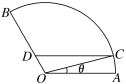
(1)用θ表示CD的长度,并写出θ的取值范围;
(2)当θ为何值时,观光道路最长?
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用![]() 表示CD的长度的关键是在
表示CD的长度的关键是在![]() 中正确利用正弦定理;
中正确利用正弦定理;
(2)首先将道路长度![]() 表达成
表达成![]() 的函数关系式,再利用导数方法研究函数的最大值,从而可以求得
的函数关系式,再利用导数方法研究函数的最大值,从而可以求得![]() 时,观光道路最长.
时,观光道路最长.
(1)在△OCD中,由正弦定理,得
![]() =
=![]() =
=![]() =
=![]() ,
,
所以CD=![]() sin
sin![]() =cos θ+
=cos θ+![]() sin θ,OD=
sin θ,OD=![]() sin θ,
sin θ,
因为OD<OB,即![]() sin θ<1,所以sin θ<
sin θ<1,所以sin θ<![]() ,所以0<θ<
,所以0<θ<![]() ,
,
所以CD=cos θ+![]() sin θ,θ的取值范围为
sin θ,θ的取值范围为![]() .
.
(2)设观光道路长度为L(θ),
则L(θ)=BD+CD+弧CA的长
=1-![]() sin θ+cos θ+
sin θ+cos θ+![]() sin θ+θ
sin θ+θ
=cos θ-![]() sin θ+θ+1,θ∈
sin θ+θ+1,θ∈![]() ,
,
L′(θ)=-sin θ-![]() cos θ+1,
cos θ+1,
由L′(θ)=0,得sin![]() =
=![]() ,
,
又θ∈![]() ,所以θ=
,所以θ=![]() ,
,
列表:
θ |
|
|
|
L′(θ) | + | 0 | - |
L(θ) | 增函数 | 极大值 | 减函数 |
所以当θ=![]() 时,L(θ)达到最大值,即当θ=
时,L(θ)达到最大值,即当θ=![]() 时,观光道路最长.
时,观光道路最长.

【题目】为了调查国企员工对新个税法的满意程度,研究人员在![]() 地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布表,其中
地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布表,其中![]() .(计算结果保留两位小数)
.(计算结果保留两位小数)
分数 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频率 | 0.08 |
| 0.35 | 0.27 |
|
(1)试估计被调查的员工的满意程度的中位数;
(2)若把每组的组中值作为该组的满意程度,试估计被调查的员工的满意程度的平均数.