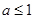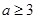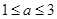题目内容
(本题14分)设函数 的定义域为
的定义域为 ,
,
(Ⅰ)若 ,求
,求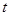 的取值范围;
的取值范围;
(Ⅱ)求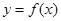 的最大值与最小值,并求出最值时对应的
的最大值与最小值,并求出最值时对应的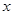 的值.
的值.
 的定义域为
的定义域为 ,
,(Ⅰ)若
 ,求
,求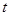 的取值范围;
的取值范围;(Ⅱ)求
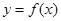 的最大值与最小值,并求出最值时对应的
的最大值与最小值,并求出最值时对应的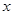 的值.
的值.(Ⅰ)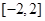
(Ⅱ)当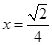 时,
时,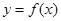 有最小值
有最小值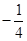 ;当
;当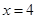 时,
时,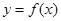 有最大值
有最大值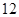 .
.
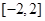
(Ⅱ)当
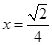 时,
时,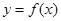 有最小值
有最小值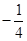 ;当
;当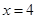 时,
时,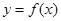 有最大值
有最大值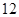 .
.试题分析:(Ⅰ)因为
 ,而
,而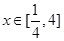 ,
,所以
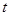 的取值范围为区间
的取值范围为区间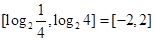 . ……6分
. ……6分(Ⅱ)记
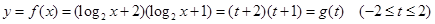 .……7分
.……7分∵
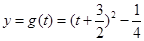 在区间
在区间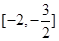 是减函数,在区间
是减函数,在区间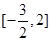 是增函数, ……8分∴当
是增函数, ……8分∴当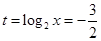 即
即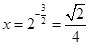 时,
时,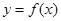 有最小值
有最小值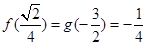 ; ……11分
; ……11分当
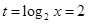 即
即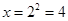 时,
时,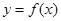 有最大值
有最大值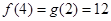 . ……14分
. ……14分点评:换元法经常考查应用,要特别注意换元前后变量的范围是否发生了变化.

练习册系列答案
相关题目
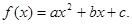
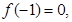 试判断函数
试判断函数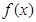 零点个数;
零点个数;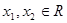 ,且
,且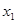 <
<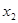 ,
,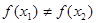 (
(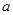 >0),试证明:
>0),试证明: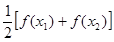 >
>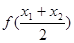 成立。
成立。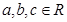 ,使
,使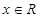 ,
,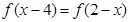 ,且
,且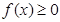 ②对任意的
②对任意的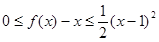 ?若存在,求出
?若存在,求出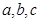 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。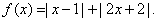
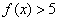 ;
;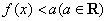 的解集为空集,求
的解集为空集,求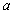 的取值范围.
的取值范围.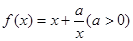 .
.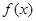 在定义域上的单调性;
在定义域上的单调性;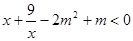 在
在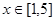 上恒成立时的实数
上恒成立时的实数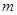 的取值范围?
的取值范围?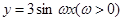 在区间
在区间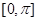 恰有2个零点,则
恰有2个零点,则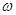 的取值范围是( )
的取值范围是( )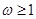
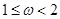
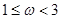
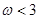
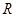 上的函数
上的函数 是最小正周期为
是最小正周期为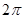 的偶函数,当
的偶函数,当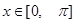 时,
时,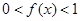 ,且在
,且在 上单调递减,在
上单调递减,在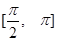 上单调递增,则函数
上单调递增,则函数 在
在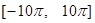 上的零点个数为 .
上的零点个数为 . 的零点一定位于区间( )
的零点一定位于区间( )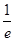 ,1)
,1)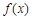 满足
满足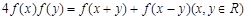 ,且
,且 ,
,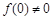 ,则下列等式不成立的是( )
,则下列等式不成立的是( )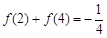
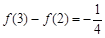
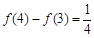
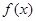 在
在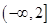 为增函数,且
为增函数,且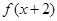 是
是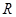 上的偶函数,若
上的偶函数,若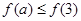 ,则实数
,则实数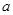 的取值范围是
的取值范围是