题目内容
【题目】在平面直角坐标系![]() 中,一个动圆经过点
中,一个动圆经过点![]() 且与直线
且与直线![]() 相切,设该动圆圆心的轨迹为曲线
相切,设该动圆圆心的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作直线交曲线
作直线交曲线![]() 于
于![]() ,
,![]() 两点,问曲线
两点,问曲线![]() 上是否存在一个定点
上是否存在一个定点![]() ,使得点
,使得点![]() 在以
在以![]() 为直径的圆上?若存在,求出点
为直径的圆上?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)存在;定点
(2)存在;定点![]()
【解析】
(1)根据抛物线定义,即可求得轨迹方程;
(2)设出直线方程,联立抛物线方程,由韦达定理,结合![]() ,即可恒成立问题,即可求得
,即可恒成立问题,即可求得![]() 点坐标.
点坐标.
(1)由题意,圆心到点![]() 的距离与到直线
的距离与到直线![]() 的距离相等,
的距离相等,
根据抛物线的定义可知,圆心的轨迹方程是![]() .
.
(2)因为过点![]() 的直线交曲线
的直线交曲线![]() 于
于![]() ,
,![]() 两点,
两点,
所以可设直线方程为![]() ,
, ,
,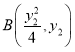 ,
,
由![]() 整理得
整理得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
假设存在定点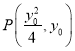 满足题意,显然
满足题意,显然![]() 且
且![]() ,
,
则![]() ,即
,即![]() .
.
因为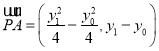 ,
,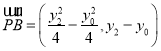 ,
,
所以![]() ,
,
即![]() ,
,
因为![]() 且
且![]() ,所以
,所以![]() ,
,
即![]() ,
,
所以![]() ,即
,即![]() ,
,
上式要恒成立,所以![]() ,即定点
,即定点![]() .
.
综上所述,存在定点![]() 满足题意.
满足题意.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
【题目】若养殖场每个月生猪的死亡率不超过![]() ,则该养殖场考核为合格,该养殖场在2019年1月到8月养殖生猪的相关数据如下表所示:
,则该养殖场考核为合格,该养殖场在2019年1月到8月养殖生猪的相关数据如下表所示:
月份 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 |
月养殖量/千只3 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 12 |
月利润/十万元 | 3.6 | 4.1 | 4.4 | 5.2 | 6.2 | 7.5 | 7.9 | 9.1 |
生猪死亡数/只 | 29 | 37 | 49 | 53 | 77 | 98 | 126 | 145 |
(1)从该养殖场2019年2月到6月这5个月中任意选取3个月,求恰好有2个月考核获得合格的概率;
(2)根据1月到8月的数据,求出月利润y(十万元)关于月养殖量x(千只)的线性回归方程(精确到0.001).
(3)预计在今后的养殖中,月利润与月养殖量仍然服从(2)中的关系,若9月份的养殖量为1.5万只,试估计:该月利润约为多少万元?
附:线性回归方程![]() 中斜率和截距用最小二乘法估计计算公式如下:
中斜率和截距用最小二乘法估计计算公式如下: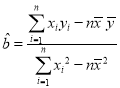 ,
,![]()
参考数据:![]() .
.