Question

已知p：x²-4x+3<0，q：x²-(m+1)x+m<0，(m>1).

（1）求不等式x²-4x+3<0的解集；

（2）若p是q的充分不必要条件，求m的取值范围.

 

 

Answer 1

【答案】

解：（1）因为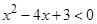，所以.

所求解集为.  ……………………………………………………… 3分

（2）当m >1时，

x²-(m+1)x+m<0的解是1<x<m，  ………………………………………………… 5分

因为p是q的充分不必要条件，

所以x²-4x+3<0的解集是x²-(m+1)x+m<0，(m>1) 解集的真子集.

所以.    ……………………………………………………………………… 7分

    当m <1时，

x²-(m+1)x+m<0的解是m <x<1，

因为p是q的充分不必要条件，

所以x²-4x+3<0的解集是x²-(m+1)x+m<0，(m<1) 解集的真子集.

    因为当m <1时 ∩= Ø，

所以m <1时p是q的充分不必要条件不成立.

综上，m的取值范围是(3，+∞). …………………………………………………10分

【解析】略