题目内容
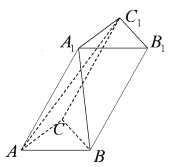
【题目】在三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 与
与![]() 所成角的余弦值为( )
所成角的余弦值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
连结A1C,交AC1于点E,取BC的中点D,连结AD、DE.证出DE是△A1BC的中位线,得DE![]() A1B,因此AE、ED所成的锐角或直角就是A1B与AC1所成的角.然后利用题中数据在△AED中分别算出边AE、ED、AD的长,根据余弦定理列式,即可算出异面直线A1B与AC1所成角的余弦值.
A1B,因此AE、ED所成的锐角或直角就是A1B与AC1所成的角.然后利用题中数据在△AED中分别算出边AE、ED、AD的长,根据余弦定理列式,即可算出异面直线A1B与AC1所成角的余弦值.
连结A1C,交AC1于点E,取BC的中点D,连结AD、DE,
∵四边形AA1C1C是平行四边形,∴E是A1C的中点
∵D是BC的中点,∴DE是△A1BC的中位线,可得DE![]() A1B,
A1B,
因此,∠AED(或其补角)就是异面直线A1B与AC1所成的角.
设AB=AC=![]() AA1=2,∵∠A1AB=60°,可得A1B=
AA1=2,∵∠A1AB=60°,可得A1B=![]() ,且∠A1BA=90°
,且∠A1BA=90°
∴△A1BA是直角三角形,得DE![]() A1B=
A1B=![]() .
.
同理,直角△A1CA中, AE![]() ,
,
又∵∠BAC=90°,AB=AC=2,D为BC中点,
∴AD![]() BC
BC![]()
由此可得△ADE中,cos∠AED![]() .
.
即异面直线A1B与AC1所成角的余弦值为![]() .
.
故选:C.

练习册系列答案
相关题目