题目内容
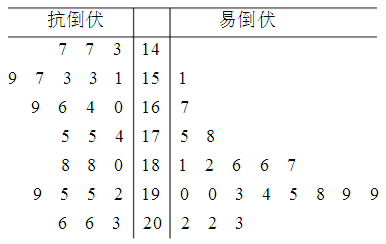
【题目】如图,四边形![]() 是直角梯形,
是直角梯形, ![]() ,又
,又![]() ,直线
,直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() .
.

(1)求证: ![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析.(2)![]() .
.
【解析】试题分析:方法1:(1)∵![]() ,∴
,∴![]() 平面ABC,∴
平面ABC,∴![]() .5分
.5分
(2)取BC的中点N,连MN.∵![]() ,∴
,∴![]() ,∴
,∴![]() 平面ABC.作
平面ABC.作![]()
![]() ,交AC的延长线于H,连结MH.由三垂线定理得
,交AC的延长线于H,连结MH.由三垂线定理得![]() ,∴
,∴![]() 为二面角
为二面角![]() 的平面角.∵直线AM与直线PC所成的角为
的平面角.∵直线AM与直线PC所成的角为![]() ,∴在
,∴在![]() 中,
中, ![]() .
.
在![]() 中,
中, ![]() .
.
在![]() 中,
中, ![]() .
.
在![]() 中,
中, ![]() .
.
在![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.
故二面角![]() 的余弦值为
的余弦值为![]() .13分
.13分
方法2:(1)∵![]() ,∴
,∴![]() 平面ABC,∴
平面ABC,∴![]() .5分
.5分
(2)在平面ABC内,过C作BC的垂线,并建立空间直角坐标系如图所示.设![]() ,则
,则![]() .
. 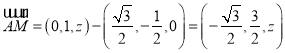 . 5分
. 5分
∵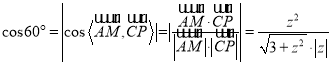 ,
,
且![]() ,∴
,∴![]() ,得
,得![]() ,∴
,∴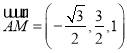 . 8分
. 8分
设平面MAC的一个法向量为![]() ,则由
,则由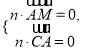 得
得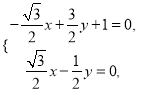 得
得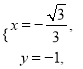 ∴
∴ . 10分
. 10分
平面ABC的一个法向量为![]() .
. 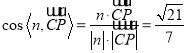 12分
12分
显然,二面角![]() 为锐二面角,∴二面角
为锐二面角,∴二面角![]() 的余弦值为
的余弦值为![]() .13分
.13分

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
【题目】某港口有一个泊位,现统计了某月100艘轮船在该泊位停靠的时间(单位:小时),如果停靠时间不足半小时按半小时计时,超过半小时不足1小时按1小时计时,以此类推,统计结果如表:
停靠时间 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
轮船数量 | 12 | 12 | 17 | 20 | 15 | 13 | 8 | 3 |
(Ⅰ)设该月100艘轮船在该泊位的平均停靠时间为![]() 小时,求
小时,求![]() 的值;
的值;
(Ⅱ)假定某天只有甲、乙两艘轮船需要在该泊位停靠![]() 小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.
小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.