题目内容
(本小题满分12分)
如图所示,已知S是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△SAB上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF的位置关系,并给予证明.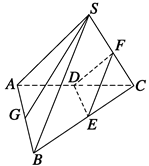
如图所示,已知S是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△SAB上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF的位置关系,并给予证明.

根据DE是△ABC的中位线,那么可知DE∥AB,同理可知DH∥AG,那么FH∥SG,结合线面平行的判定定理得到证明。
试题分析:SG∥平面DEF,证明如下:
方法一 连接CG交DE于点H,
如图所示.
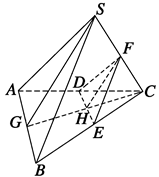
∵DE是△ABC的中位线,
∴DE∥AB.
在△ACG中,D是AC的中点,
且DH∥AG.
∴H为CG的中点.
∴FH是△SCG的中位线,
∴FH∥SG.
又SG
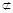 平面DEF,FH
平面DEF,FH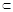 平面DEF,
平面DEF,∴SG∥平面DEF.
点评:解决线面位置关系,要考虑线面平行和垂直的两个特殊情况, 结合已知的判定定理和性质定理来分析,属于中档题。

练习册系列答案
相关题目
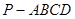 的底面是边长为6的正方形,侧棱
的底面是边长为6的正方形,侧棱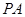 的长为8,且垂直于底面,点
的长为8,且垂直于底面,点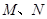 分别是
分别是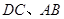 的中点.求
的中点.求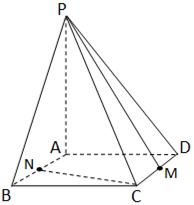
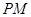 与
与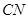 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);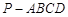 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形, 是棱
是棱 上的动点.
上的动点.
 是
是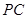 //平面
//平面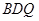 ;
;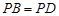 ,求证:
,求证: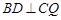 ;
; ,求四棱锥
,求四棱锥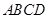 所在平面与平面
所在平面与平面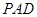 垂直,
垂直,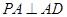 ,且
,且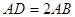 ,
,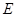 为
为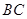 上的动点.
上的动点.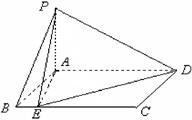
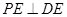 ;
;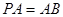 ,在线段
,在线段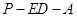 的大小为
的大小为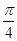 . 若存在,确定点E的位置,若不存在,说明理由.
. 若存在,确定点E的位置,若不存在,说明理由.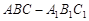 中,
中,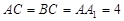 ,
, 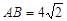 ,若
,若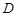 是
是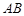 中点.
中点.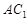 ∥平面
∥平面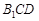 ;
; 所成的角.
所成的角. 、
、 是两条不同的直线,
是两条不同的直线, 、
、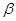 是两个不同的平面,则下列命题中正确的是
是两个不同的平面,则下列命题中正确的是 ,且
,且 ,则
,则
 ,且
,且 ,则
,则
 ,且
,且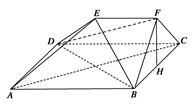
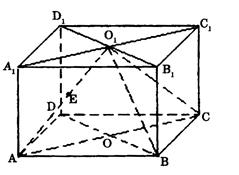
 平面O1BD
平面O1BD