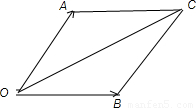
题目内容
已知|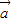 |=|
|=| |=2,
|=2,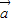 与
与 的夹角为
的夹角为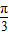 ,则
,则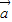 +
+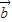 在
在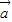 上的投影为 .
上的投影为 .
【答案】分析:根据两个向量的模长和夹角做出两个向量的和的模长,看出两个向量的和与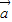 的夹角,有向量的夹角和模长用向量的投影公式得到结果.
的夹角,有向量的夹角和模长用向量的投影公式得到结果.
解答:解:∵|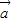 |=|
|=|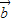 |=2,
|=2,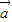 与
与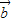 的夹角为
的夹角为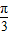
∴|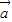 +
+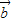 |=2×2×
|=2×2×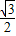 =2
=2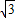
∵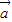 +
+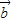 与
与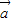 的夹角是
的夹角是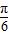 ,
,
∴ +
+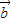 在
在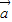 上的投影为|
上的投影为| +
+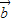 |cos
|cos =2
=2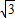 ×
×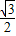 =3
=3
故答案为:3
点评:本题考查向量的投影,在计算投影的时注意看清楚是哪一个向量在哪一个向量上的投影,再用模长乘以夹角的余弦.
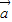 的夹角,有向量的夹角和模长用向量的投影公式得到结果.
的夹角,有向量的夹角和模长用向量的投影公式得到结果.解答:解:∵|
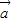 |=|
|=|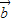 |=2,
|=2,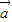 与
与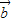 的夹角为
的夹角为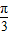
∴|
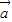 +
+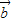 |=2×2×
|=2×2×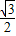 =2
=2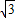
∵
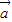 +
+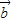 与
与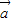 的夹角是
的夹角是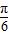 ,
,∴
 +
+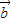 在
在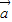 上的投影为|
上的投影为| +
+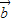 |cos
|cos =2
=2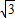 ×
×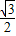 =3
=3
故答案为:3
点评:本题考查向量的投影,在计算投影的时注意看清楚是哪一个向量在哪一个向量上的投影,再用模长乘以夹角的余弦.

练习册系列答案
相关题目
已知α∈(
,π),cosα=-
,则tan(α-
)等于( )
| π |
| 2 |
| 4 |
| 5 |
| π |
| 4 |
A、
| ||
| B、7 | ||
C、-
| ||
| D、-7 |
已知-
<x<0,sinx+cosx=
,则
等于( )
| π |
| 2 |
| 1 |
| 5 |
| sinx-cosx |
| sinx+cosx |
| A、-7 | ||
B、-
| ||
| C、7 | ||
D、
|
