题目内容
7.设函数f(x)的定义域为D,若存在定义域[a,b]⊆D,使得函数f(x)在[a,b]上的值域也为[a,b],则称f(x)为“等域函数”.已知函数f(x)=ax,(a>1)为“等域函数”,则实数a的取值范围为(1,${e}^{\frac{1}{e}}$).分析 由新定义可得函数f(x)=ax,(a>1)的定义域和值域均为[m,n],即有am=m,an=n,即方程ax=x有两个不相等的实根,两边取自然对数,转化为函数的图象之间的关系,即可得到所求a的范围.
解答 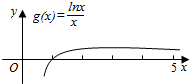 解:由新定义可得函数f(x)=ax,(a>1)的定义域和值域均为[m,n],
解:由新定义可得函数f(x)=ax,(a>1)的定义域和值域均为[m,n],
即有am=m,an=n,
即方程ax=x有两个不相等的实根,
即有lnax=lnx,
即lna=$\frac{lnx}{x}$有两个不相等的实根.
令g(x)=$\frac{lnx}{x}$,则g(x)的导数为g′(x)=$\frac{1-lnx}{{x}^{2}}$,
当x>e时,g′(x)<0,g(x)递减;
当0<x<e时,g′(x)>0,g(x)递增.
即有x=e取得最大值$\frac{1}{e}$.
则有图象可得0<lna<$\frac{1}{e}$.
解得1<a<${e}^{\frac{1}{e}}$.
故答案为:(1,${e}^{\frac{1}{e}}$).
点评 本题考查新定义的理解和运用,考查函数的单调性的运用,以及导数的运用:求单调区间和极值、最值,属于中档题.

练习册系列答案
相关题目
15.三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,N是BC的中点,点P在A1B1上,且满足$\overrightarrow{{A_1}P}$=λ$\overrightarrow{{A_1}{B_1}}$,直线PN与平面ABC所成角θ的正切值取最大值时λ的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
2. 如图,长沙河西先导区某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的矩形绿化区,这三块绿化区四周和绿化区之间设有1米宽的走道.已知三块绿化区的总面积为800平方米,则该矩形区域ABCD占地面积的最小值为( )平方米.
如图,长沙河西先导区某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的矩形绿化区,这三块绿化区四周和绿化区之间设有1米宽的走道.已知三块绿化区的总面积为800平方米,则该矩形区域ABCD占地面积的最小值为( )平方米.
 如图,长沙河西先导区某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的矩形绿化区,这三块绿化区四周和绿化区之间设有1米宽的走道.已知三块绿化区的总面积为800平方米,则该矩形区域ABCD占地面积的最小值为( )平方米.
如图,长沙河西先导区某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的矩形绿化区,这三块绿化区四周和绿化区之间设有1米宽的走道.已知三块绿化区的总面积为800平方米,则该矩形区域ABCD占地面积的最小值为( )平方米.| A. | 900 | B. | 920 | C. | 948 | D. | 968 |
12.已知不等式组$\left\{\begin{array}{l}{x+y≥4}\\{x-y≥-2}\\{x≤2}\end{array}\right.$,表示的平面区域为D,点O(0,0),A(1,0).若点M是D上的动点,则$\frac{\overrightarrow{OA}•\overrightarrow{OM}}{|\overrightarrow{OM|}}$的最小值是( )
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{3\sqrt{10}}{10}$ |
19.下列说法正确的是( )
| A. | 小于90°的角是锐角 | B. | 在△ABC中,若cosA=cosB,那么A=B | ||
| C. | 第二象限的角大于第一象限的角 | D. | 若角α与角β的终边相同,那么α=β |
16.已知点A(4,1,3),B(2,-5,1),C为线段AB上一点,且3|$\overrightarrow{AC}$|=|$\overrightarrow{AB}$|,则点C的坐标是( )
| A. | $(\frac{7}{2},-\frac{1}{2},\frac{5}{2})$ | B. | $(\frac{3}{8},-3,2)$ | C. | $(\frac{10}{3},-1,\frac{7}{3})$ | D. | $(\frac{5}{2},-\frac{7}{2},\frac{3}{2})$ |
17.函数f(x)=x+2cosx在[0,π]上的极小值点为( )
| A. | 0 | B. | $\frac{π}{6}$ | C. | $\frac{5π}{6}$ | D. | π |