题目内容
(本题满分12分)
已知函数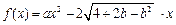 ,
,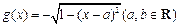 .
.
(1)当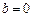 时,若
时,若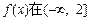 上单调递减,求a的取值
上单调递减,求a的取值 范围;
范围;
(2)求满足下列条件的所有整数对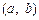 :存在
:存在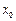 ,使得
,使得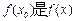 的最大值,
的最大值,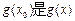 的最小值;
的最小值;
已知函数
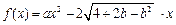 ,
,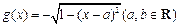 .
.(1)当
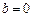 时,若
时,若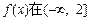 上单调递减,求a的取值
上单调递减,求a的取值 范围;
范围;(2)求满足下列条件的所有整数对
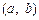 :存在
:存在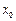 ,使得
,使得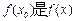 的最大值,
的最大值,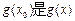 的最小值;
的最小值;1)当
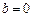 时,
时, ,…………………………………………………1分
,…………………………………………………1分
若 ,
,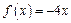 ,则
,则 在
在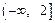 上单调递减,符合题意;………3分
上单调递减,符合题意;………3分
若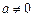 ,要使
,要使 在
在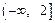 上单调递减,
上单调递减,
必须满足 ……………………………………………………………………5分
……………………………………………………………………5分
∴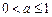
 .综上所述,a的取值范围是
.综上所述,a的取值范围是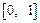 …………………………………6分
…………………………………6分
(2)若 ,
, ,则
,则 无
无 最大值,………………………
最大值,……………………… 7分
7分
故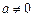 ,∴
,∴ 为二次函数,
为二次函数,
要使 有最大值,必须满足
有最大值,必须满足 即
即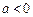 且
且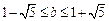 ,…8分
,…8分
此时,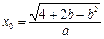 时,
时, 有最大值.…………………………分
有最大值.…………………………分
又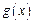 取最小值时,
取最小值时,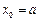 ,………………………………………………………分
,………………………………………………………分
依题意,有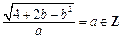 ,则
,则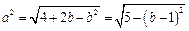 ,…………分
,…………分
∵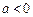 且
且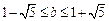 ,∴
,∴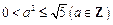 ,得
,得 ,………………分
,………………分
此时 或
或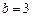 .
.
∴满足条件的整数对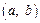 是
是 .……………………………12分
.……………………………12分

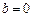 时,
时, ,…………………………………………………1分
,…………………………………………………1分若
 ,
,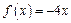 ,则
,则 在
在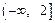 上单调递减,符合题意;………3分
上单调递减,符合题意;………3分若
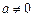 ,要使
,要使 在
在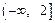 上单调递减,
上单调递减,必须满足
 ……………………………………………………………………5分
……………………………………………………………………5分∴
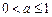
 .综上所述,a的取值范围是
.综上所述,a的取值范围是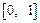 …………………………………6分
…………………………………6分(2)若
 ,
, ,则
,则 无
无 最大值,………………………
最大值,……………………… 7分
7分故
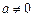 ,∴
,∴ 为二次函数,
为二次函数,要使
 有最大值,必须满足
有最大值,必须满足 即
即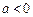 且
且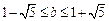 ,…8分
,…8分此时,
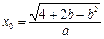 时,
时, 有最大值.…………………………分
有最大值.…………………………分又
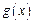 取最小值时,
取最小值时,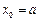 ,………………………………………………………分
,………………………………………………………分依题意,有
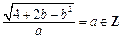 ,则
,则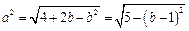 ,…………分
,…………分∵
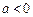 且
且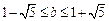 ,∴
,∴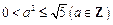 ,得
,得 ,………………分
,………………分此时
 或
或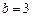 .
.∴满足条件的整数对
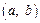 是
是 .……………………………12分
.……………………………12分略

练习册系列答案
相关题目
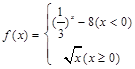 ,若f(a)>1,则实数a的取值范围是( )
,若f(a)>1,则实数a的取值范围是( )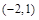
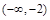 ∪
∪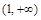
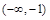 ∪(0,+∞)
∪(0,+∞)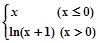 ,若f(2-x2)>f(x),则实数x的取值范围是( )
,若f(2-x2)>f(x),则实数x的取值范围是( )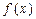 ,如果满足:对任意
,如果满足:对任意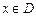 ,存在常数
,存在常数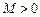 ,都有
,都有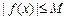 成立,则称
成立,则称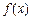 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数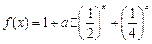 ;
;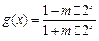 .
.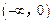 上的值域,并判断函数
上的值域,并判断函数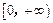 上是以3为上界的
上是以3为上界的 有界函数,求实数a的取值范围;
有界函数,求实数a的取值范围;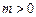 ,函
,函 数
数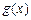 在
在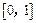 上的上界是
上的上界是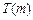 ,求
,求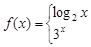
 ,则
,则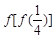 的值是( )
的值是( )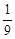

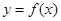 的定义域是
的定义域是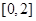 ,则函数
,则函数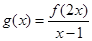 的定义域是( )
的定义域是( )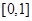


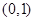
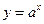 (
(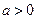 且
且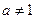 )与函数
)与函数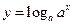 (
(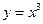 与
与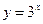 的值域相同;③函数
的值域相同;③函数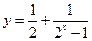 与
与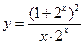 都是奇函数;④
都是奇函数;④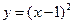 与
与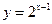 在区间
在区间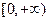 上都是增函数,其中正确命题的序号是_____________。(把你认为正确的命题序号都填上)
上都是增函数,其中正确命题的序号是_____________。(把你认为正确的命题序号都填上)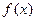 ,
,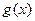 分别由下表给出
分别由下表给出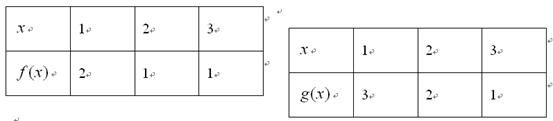
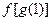 的值为 ;当
的值为 ;当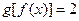 时,
时, .
. 2+(K-1)x+3是偶函数,则f(x)的递减区间是
2+(K-1)x+3是偶函数,则f(x)的递减区间是