题目内容
【题目】在平面直角坐标系xOy中，直线l的参数方程为
(t为参数，a∈R).在以坐标原点为极点，x轴的非负半轴为极轴的极坐标系中，曲线C的极坐标方程为
.
（1）若点A(0，4)在直线l上，求直线l的极坐标方程；
（2）已知a>0，若点P在直线l上，点Q在曲线C上，若|PQ|最小值
为，求a的值.
【答案】（1）
（2）
【解析】
（1）将直线l参数方程转化为直角坐标方程，再将A点坐标代入即可求出a值，进而求出极坐标方程.
（2）设直线m平行于直线l，则直线m与曲线C的切点到直线l的距离即为|PQ|最小值，计算求解即可.
（1）由直线l的参数方程为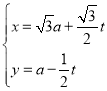
(t为参数，a∈R)可得，
直线l的直角坐标方程为
，
因为点A(0，4)在直线l上，代入方程，得
则直线l的直角坐标方程为
，
将
代入，得
即直线l的极坐标方程为
（2）将曲线C的极坐标方程
化为直角坐标方程，得
，
设直线
，
则直线m与曲线C的切点（靠近直线l）到直线
的距离即为|PQ|最小值，
将直线m代入曲线C中，得
，
由相切，得
，即
（舍负），
由于直线m与直线l的距离为
，
则
，
活力课时同步练习册系列答案
【题目】在世界读书日期间，某地区调查组对居民阅读情况进行了调查，获得了一个容量为200的样本，其中城镇居民140人，农村居民60人.在这些居民中，经常阅读的城镇居民有100人，农村居民有30人.
（1）填写下面列联表，并判断能否有99%的把握认为经常阅读与居民居住地有关？
城镇居民 | 农村居民 | 合计 | |
经常阅读 | 100 | 30 | |
不经常阅读 | |||
合计 | 200 |
（2）调查组从该样本的城镇居民中按分层抽样抽取出7人，参加一次阅读交流活动，若活动主办方从这7位居民中随机选取2人作交流发言，求被选中的2位居民都是经常阅读居民的概率.
附：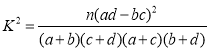
，其中
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
