题目内容
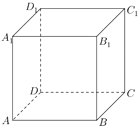
【题目】在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且![]() ;
;

求证:(1)点E,F,G,H四点共面;
(2)直线EH,BD,FG相交于同一点.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据题意利用中位线定理,平行线分线段成比例逆定理和平行公理,可得![]() ,再根据公理2的推论即得证;
,再根据公理2的推论即得证;
(2)由(1)知![]() 且
且![]() ,所以EH与FG交于一点P,只需再证明点P在直线BD上,即可证出.
,所以EH与FG交于一点P,只需再证明点P在直线BD上,即可证出.

(1)如图所示,连接EF,HG,
空间四边形ABCD中,H、G分别是AD、CD的中点,
∴![]() 且
且![]() .
.
又![]() ,∴
,∴![]() 且
且![]() .
.
故![]() ,即E、F、G、H四点共面.
,即E、F、G、H四点共面.
(2)由(1)知![]() 且
且![]() ,
,
∴设EH与FG交于点P,
∵![]() 平面ABD,P在平面ABD内,
平面ABD,P在平面ABD内,
同理P在平面BCD内,且平面![]() 平面
平面![]() ,
,
∴点P在直线BD上,
∴直线EH,BD,FG相交于一点.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了了解某高校大学生是否愿意做志愿者.某调查机构从该高校访问了80人,经过统计,得到如下丢失数据的列联表:(![]() ,表示丢失的数据)
,表示丢失的数据)
无意愿 | 有意愿 | 总计 | |
男 | a | b | 40 |
女 | 5 | d | A |
总计 | 25 | B | 80 |
(1)求出![]() 的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
(2)若表中无意愿做志愿者的5个女同学中,3个是大学三年级同学,2个是大学四年级同学.现从这5个同学中随机选2同学进行进一步调查,求这2个同学是同年级的概率.
附:参考公式及数据:
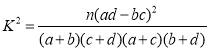 ,其中
,其中![]()
| 0.40 | 0.25 | 0.10 | 0.010 | 0.005 | 0.001 |
| 0.708 | l.323 | 2.706 | 6.635 | 7.879 | 10.828 |
【题目】已知焦点在y轴上的椭圆E的中心是原点O,离心率等于![]() ,以椭圆E的长轴和短轴为对角线的四边形的周长为
,以椭圆E的长轴和短轴为对角线的四边形的周长为![]() .直线
.直线![]() 与
与![]() 轴交于点P,与椭圆E相交于A,B两个点.
轴交于点P,与椭圆E相交于A,B两个点.
(I)求椭圆E的方程;
(II)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【题目】某地区对12岁儿童瞬时记忆能力进行调查,瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为![]() .
.
视觉 | 视觉记忆能力 | ||||
偏低 | 中等 | 偏高 | 超常 | ||
听觉记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
中等 | 1 | 8 | 3 |
| |
偏高 | 2 |
| 0 | 1 | |
超常 | 0 | 2 | 1 | 1 | |
(1)试确定![]()
![]() 的值;
的值;
(2)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列
的分布列
【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.