题目内容
1.已知f(x)=cos($\sqrt{3}$x+φ)-$\sqrt{3}$sin($\sqrt{3}$x+φ)为奇函数,则φ可以取的一个值为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $-\frac{π}{6}$ | D. | $-\frac{π}{3}$ |
分析 利用两角和的余弦公式化简f(x)的解析式为f(x)=2cos($\sqrt{3}$x+φ+$\frac{π}{3}$)为奇函数,可得φ+$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈z,由此结合选项可得结论.
解答 解:根据f(x)=cos($\sqrt{3}$x+φ)-$\sqrt{3}$sin($\sqrt{3}$x+φ)=2cos[($\sqrt{3}$x+φ)+$\frac{π}{3}$]=2cos($\sqrt{3}$x+φ+$\frac{π}{3}$)为奇函数,
则φ+$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈z,即 φ=kπ+$\frac{π}{6}$,k∈z.
结合所给的选项,
故选:A.
点评 本题主要考查两角和的余弦公式,正弦函数、余弦函数的奇偶性,属于基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
16.已知直线方程为(2+m)x+(1-2m)y+4-3m=0.这条直线恒过一定点,这个定点坐标为( )
| A. | (-2m,-m-4) | B. | (5,1) | C. | (-1,-2) | D. | (2m,m+4) |
16.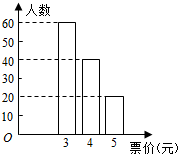 2014 年12 月28 日开始,北京市公共电汽车和地铁按照里程分段计价.具体如下表.(不考虑公交卡折扣情况)
2014 年12 月28 日开始,北京市公共电汽车和地铁按照里程分段计价.具体如下表.(不考虑公交卡折扣情况)
已知在北京地铁四号线上,任意一站到陶然亭站的票价不超过5 元,现从那些只乘坐四号线地铁,且在陶然亭出站的乘客中随机选出120 人,他们乘坐地铁的票价统计如图所示.
(Ⅰ)如果从那些只乘坐四号线地铁,且在陶然亭站出站的乘客中任选1 人,试估计此人乘坐地铁的票价小于5 元的概率;
(Ⅱ)从那些只乘坐四号线地铁,且在陶然亭站出站的乘客中随机选2 人,记x 为这2人乘坐地铁的票价和,根据统计图,并以频率作为概率,求X 的分布列和数学期望;
(Ⅲ)小李乘坐地铁从A 地到陶然亭的票价是5 元,返程时,小李乘坐某路公共电汽车所花交通费也是5 元,假设小李往返过程中乘坐地铁和公共电汽车的路程均为s 公里,试写出s 的取值范围.(只需写出结论)
 2014 年12 月28 日开始,北京市公共电汽车和地铁按照里程分段计价.具体如下表.(不考虑公交卡折扣情况)
2014 年12 月28 日开始,北京市公共电汽车和地铁按照里程分段计价.具体如下表.(不考虑公交卡折扣情况)| 乘公共汽车方案 | 10公里(含)内2元; 10公里以上部分,每增加1元可乘坐5公里(含) |
| 乘坐地铁方案(不含机场线) | 6公里(含)内3元 6公里至12公里(含)4元 12公里至22公里(含)5元 |
| 22公里至32公里(含)6元 32公里以上部分,每增加1元可乘坐20公里(含) |
(Ⅰ)如果从那些只乘坐四号线地铁,且在陶然亭站出站的乘客中任选1 人,试估计此人乘坐地铁的票价小于5 元的概率;
(Ⅱ)从那些只乘坐四号线地铁,且在陶然亭站出站的乘客中随机选2 人,记x 为这2人乘坐地铁的票价和,根据统计图,并以频率作为概率,求X 的分布列和数学期望;
(Ⅲ)小李乘坐地铁从A 地到陶然亭的票价是5 元,返程时,小李乘坐某路公共电汽车所花交通费也是5 元,假设小李往返过程中乘坐地铁和公共电汽车的路程均为s 公里,试写出s 的取值范围.(只需写出结论)
6.已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001、002、…800编号.
(1)下面摘取了随机数表的第7行到第9行
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 66 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
如果从第8行第7列的数开始向右读,请你依次写出最先检查的5个人的编号;
(2)抽取的100人的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向、纵向分别表示地理成绩与数学成绩各等级人数,例如:表中数学成绩为良好的共有20+18+4=42.在该样本中,数学成绩优秀率是30%,
在地理成绩及格的学生中,已知a≥10,b≥8,求数学成绩优秀的人数比及格的人数少的概率.
(1)下面摘取了随机数表的第7行到第9行
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 66 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
如果从第8行第7列的数开始向右读,请你依次写出最先检查的5个人的编号;
(2)抽取的100人的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向、纵向分别表示地理成绩与数学成绩各等级人数,例如:表中数学成绩为良好的共有20+18+4=42.在该样本中,数学成绩优秀率是30%,
| 人数 | 数学 | |||
| 优秀 | 良好 | 及格 | ||
地 理 | 优秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
10.复数$\frac{1+2i}{3-4i}$的虚部为( )
| A. | $-\frac{1}{5}$ | B. | $-\frac{i}{5}$ | C. | $\frac{2i}{5}$ | D. | $\frac{2}{5}$ |