题目内容
已知{an}是递增的等差数列,它的前三项的和为-3,前三项的积为8.
(1)求数列{an}的通项公式;
(2)求数列{|an|}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)求数列{|an|}的前n项和Sn.
(1)设{an}的公差为d(d>0),依题意,
…(2分),
即
,解得
或
…(4分),
因为d>0,所以
,{an}的通项an=-7+3n…(5分)
(2)由(1)得a1=-4,|a1|=4;a2=-1,|a2|=1…(6分);
当n≥3时,an>0,|an|=an…(7分),
所以S1=4,S2=5…(8分)
当n≥3时,Sn=S2+(a3+…an)=5+[2+…+(-7+3n)]…(9分)
=5+
×(n-2)
=
n2-
n+10…(11分),
综上所述,Sn=
…(12分).
|
即
|
|
|
因为d>0,所以
|
(2)由(1)得a1=-4,|a1|=4;a2=-1,|a2|=1…(6分);
当n≥3时,an>0,|an|=an…(7分),
所以S1=4,S2=5…(8分)
当n≥3时,Sn=S2+(a3+…an)=5+[2+…+(-7+3n)]…(9分)
=5+
| 2+(-7+3n) |
| 2 |
=
| 3 |
| 2 |
| 11 |
| 2 |
综上所述,Sn=
|

练习册系列答案
相关题目
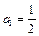 ,则
,则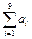 = .
= . 的前
的前 项和
项和 .
.