题目内容
已知函数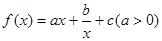
的图象在点(1，
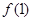)处的切线方程为
。
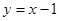(1)用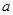
表示出
；
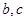(2)若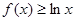
在[1，＋∞)上恒成立，求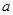的取值范围．
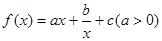的图象在点(1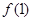，)处的切线方程为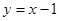。(1)用
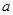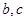表示出；(2)若
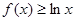在[1，＋∞)上恒成立，求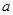的取值范围．
(ⅰ)当0<a<
时，
>1.若1<x<
，则g′(x)<0，g(x)是减函数，所以g(x)<g(1)＝0，即f(x)<ln x．故f(x)≥ln x在[1，＋∞)上不恒成立．
(ⅱ)当a≥
时，≤1.若x>1，则g′(x)>0，g(x)是增函数，所以g(x)>g(1)＝0，
即f(x)>ln x，故当x≥1时，f(x)≥ln x.
综上所述，所求a的取值范围为[
，＋∞)略
练习册系列答案
相关题目
在闭区间 [– 3，0] 上的最大值、最小值分别是（ ）
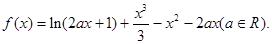
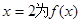的极值点，求实数a的值；
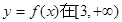上为增函数，求实数a的取值范围；
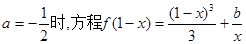有实根，求实数b的最大值。
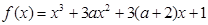有极大值和极小值，则
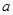的取值范围是__________．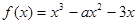 
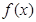在区间上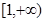
是增函数，求实数
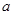的取值范围；
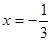是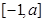
上的最大值和最小值.
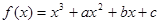,当
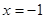时,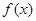
的极大值为7;当
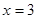时,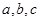
的值； (2)函数
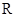上的函数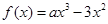
，其中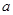
为大于零的常数．
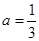时，令
，
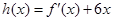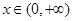时，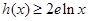
（
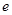为自然对数的底数）；
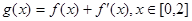，在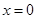
处取得最大值，求
,其中a , b , c是以d为公差的等差数列，且a＞0,d＞0.设
［1-
］上，
，在
，将点
A， B， C,
，求a ,d的值.
，若函数
(
)有小于零的极值点，则（）
