题目内容
函数 在闭区间 [– 3,0] 上的最大值、最小值分别是( )
在闭区间 [– 3,0] 上的最大值、最小值分别是( )
 在闭区间 [– 3,0] 上的最大值、最小值分别是( )
在闭区间 [– 3,0] 上的最大值、最小值分别是( )| A.1,? 1 | B.1,? 17 |
| C.3,? 17 | D.9,? 197 |
C
解:由f′(x)=3x-3=0,得x=±1,
当x<-1时,f′(x)>0,2
当-1<x<1时,f′(x)<0,
当x>1时,f′(x)>0,
故f(x)的极小值、极大值分别为f(-1)=3,f(1)=-1,
而f(-3)=-17,f(0)=1,
故函数f(x)=x3-3x+1在[-3,0]上的最大值、最小值分别是3、-17.
选C
当x<-1时,f′(x)>0,2
当-1<x<1时,f′(x)<0,
当x>1时,f′(x)>0,
故f(x)的极小值、极大值分别为f(-1)=3,f(1)=-1,
而f(-3)=-17,f(0)=1,
故函数f(x)=x3-3x+1在[-3,0]上的最大值、最小值分别是3、-17.
选C

练习册系列答案
相关题目
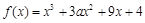 在
在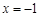 时有极值.
时有极值.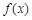 的解析式;
的解析式;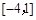 上的最大值、最小值.
上的最大值、最小值. 的极大值点是( )
的极大值点是( )


 在区间
在区间 上的最大值与最小值分别为
上的最大值与最小值分别为 ,则
,则 _____________.
_____________.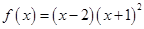 在区间
在区间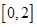 上的值域为( )
上的值域为( )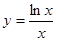 的最大值为( )
的最大值为( )



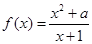 在
在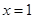 处取极值,则
处取极值,则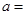 __________.
__________. 在[
在[ ]上的最大值为
]上的最大值为 ,则m的值 .
,则m的值 .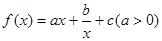 的图象在点(1,
的图象在点(1,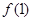 )处的切线方程为
)处的切线方程为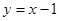 。
。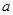 表示出
表示出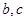 ;
;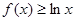 在[1,+∞)上恒成立,求
在[1,+∞)上恒成立,求