题目内容
【题目】在平面直角坐标系中,动点P(x,y)到两条坐标轴的距离之和等于它到点(1,1)的距离,记点P的轨迹为曲线W,给出下列四个结论: ①曲线W关于原点对称;
②曲线W关于直线y=x对称;
③曲线W与x轴非负半轴,y轴非负半轴围成的封闭图形的面积小于 ![]() ;
;
④曲线W上的点到原点距离的最小值为2﹣ ![]()
其中,所有正确结论的序号是 .
【答案】②③④
【解析】解:∵动点P(x,y)到两条坐标轴的距离之和等于它到点(1,1)的距离, ∴|x|+|y|= ![]() ,
,
∴|xy|+x+y﹣1=0,
∴xy>0,(x+1)(y+1)=2或xy<0,(y﹣1)(1﹣x)=0,
函数的图象如图所示
∴曲线W关于直线y=x对称;
曲线W与x轴非负半轴,y轴非负半轴围成的封闭图形的面积小于 ![]() ;
;
由y=x与(x+1)(y+1)=2联立可得x= ![]() ﹣1,∴曲线W上的点到原点距离的最小值为
﹣1,∴曲线W上的点到原点距离的最小值为 ![]() (
( ![]() ﹣1)=2﹣
﹣1)=2﹣ ![]() ,
,
∴所有正确结论的序号是②③④.
所以答案是:②③④.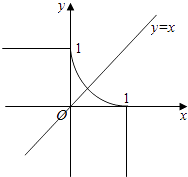

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目

