题目内容
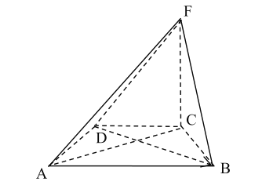
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 是椭圆上一动点(与左、右顶点不重合)已知
是椭圆上一动点(与左、右顶点不重合)已知![]() 的内切圆半径的最大值为
的内切圆半径的最大值为![]() ,椭圆的离心率为
,椭圆的离心率为![]() .
.
(1)求椭圆C的方程;
(2)过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,过
两点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 与另一点
与另一点![]() (
(![]() 不与
不与![]() 重合).设
重合).设![]() 的外心为
的外心为![]() ,求证
,求证![]() 为定值.
为定值.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)当![]() 面积最大时,
面积最大时,![]() 最大,即
最大,即![]() 点位于椭圆短轴顶点时
点位于椭圆短轴顶点时![]() ,即可得到
,即可得到![]() 的值,再利用离心率求得
的值,再利用离心率求得![]() ,即可得答案;
,即可得答案;
(2)由题意知,直线![]() 的斜率存在,且不为0,设直线
的斜率存在,且不为0,设直线![]() 为
为![]() ,代入椭圆方程得
,代入椭圆方程得![]() .设
.设![]() ,利用弦长公式求得
,利用弦长公式求得![]() ,利用
,利用![]() 的垂直平分线方程求得
的垂直平分线方程求得![]() 的坐标,两个都用
的坐标,两个都用![]() 表示,代入
表示,代入![]() 中,即可得答案.
中,即可得答案.
(1)由题意知:![]() ,∴
,∴![]() ,∴
,∴![]() .
.
设![]() 的内切圆半径为
的内切圆半径为![]() ,
,
则![]() ,
,
故当![]() 面积最大时,
面积最大时,![]() 最大,即
最大,即![]() 点位于椭圆短轴顶点时
点位于椭圆短轴顶点时![]() ,
,
所以![]() ,把
,把![]() 代入,解得:
代入,解得:![]() ,
,
所以椭圆方程为![]() .
.
(2)由题意知,直线![]() 的斜率存在,且不为0,设直线
的斜率存在,且不为0,设直线![]() 为
为![]() ,
,
代入椭圆方程得![]() .
.
设![]() ,则
,则![]() ,
,
所以![]() 的中点坐标为
的中点坐标为![]() ,
,
所以![]() .
.
因为![]() 是
是![]() 的外心,所以
的外心,所以![]() 是线段
是线段![]() 的垂直平分线与线段
的垂直平分线与线段![]() 的垂直平分线的交点,
的垂直平分线的交点,![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() ,所以
,所以![]()
所以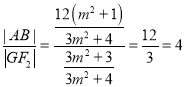 ,所以
,所以![]() 为定值,定值为4.
为定值,定值为4.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:

(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
【题目】微信运动,是由腾讯开发的一个类似计步数据库的公众账号.用户可以通过关注微信运动公众号查看自己每天行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.微信运动公众号为了解用户的一些情况,在微信运动用户中随机抽取了100名用户,统计了他们某一天的步数,数据整理如下:
或点赞.微信运动公众号为了解用户的一些情况,在微信运动用户中随机抽取了100名用户,统计了他们某一天的步数,数据整理如下:
|
|
|
|
|
|
|
| 5 | 20 | 50 | 15 | 5 | 5 |
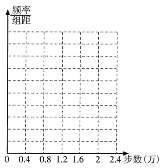
(1)根据表中数据,在如图所示的坐标平面中作出其频率分布直方图,并在纵轴上标明各小长方形的高;
(2)若视频率分布为概率分布,在微信运动用户中随机抽取3人,求至少2人步数多于1.2万步的概率;
(3)若视频率分布为概率分布,在微信运动用户中随机抽取2人,其中每日走路不超过0.8万步的有![]() 人,超过1.2万步的有
人,超过1.2万步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.