题目内容
定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有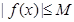 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的上界.
的上界.
(1)判断函数 是否是有界函数,请写出详细判断过程;
是否是有界函数,请写出详细判断过程;
(2)试证明:设 ,若
,若 在
在 上分别以
上分别以 为上界,
为上界,
求证:函数 在
在 上以
上以 为上界;
为上界;
(3)若函数 在
在 上是以3为上界的有界函数,
上是以3为上界的有界函数,
求实数 的取值范围.
的取值范围.
(1) 是有界函数(2)见解析(3)
是有界函数(2)见解析(3)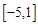
解析试题分析:(1)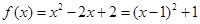 ,当
,当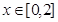 时,
时,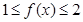
则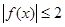 ,由有界函数定义可知
,由有界函数定义可知 是有界函数
是有界函数
(2)由题意知对任意 ,存在常数
,存在常数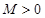 ,都有
,都有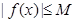 成立
成立
即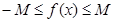 ,同理
,同理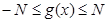 (常数
(常数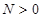 )
)
则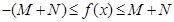 ,即
,即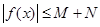
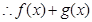 在
在 上以
上以 为上界
为上界
(3)由题意知,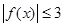 在
在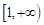 上恒成立。
上恒成立。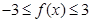 ,
, 
∴ 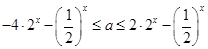 在
在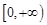 上恒成立
上恒成立
∴ 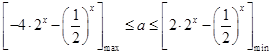
设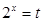 ,
,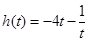 ,
,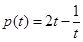 ,由
,由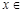
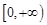 得 t≥1,
得 t≥1,
设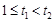 ,
, ,
,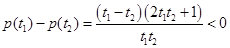
所以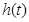 在
在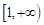 上递减,
上递减,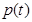 在
在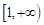 上递增,(单调性不证,不扣分)
上递增,(单调性不证,不扣分)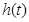 在
在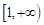 上的最大值为
上的最大值为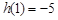 ,
, 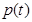 在
在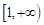 上的最小值为
上的最小值为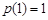 。
。
所以实数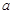 的取值范围为
的取值范围为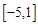
考点:二次函数求最值及不等式恒成立问题
点评:不等式恒成立转化为求函数最值问题,利用单调性可求最值

练习册系列答案
相关题目
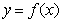 是定义在
是定义在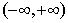 上的偶函数,当
上的偶函数,当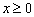 时,
时, 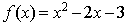 。
。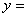
 在
在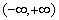 上的解析式;
上的解析式;  的大致图象;并根据图像写出
的大致图象;并根据图像写出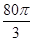 立方米,且
立方米,且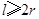 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为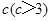 千元,设该容器的建造费用为
千元,设该容器的建造费用为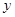 千元.
千元.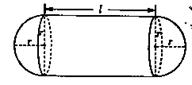
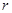 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;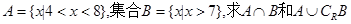

 ,
, 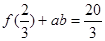 ,且
,且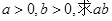 的取值范围
的取值范围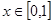 时,
时, 恒成立,且
恒成立,且 的取值范围
的取值范围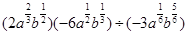 ;
;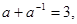 求
求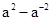 的值.
的值. 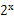 -2,若同时满足条件:
-2,若同时满足条件: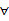 x∈R,f(x) <0或g(x) <0;②
x∈R,f(x) <0或g(x) <0;②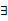 x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。

 的图像上有与
的图像上有与 轴平行的切线,求
轴平行的切线,求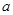 的取值范围。
的取值范围。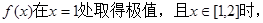
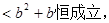 求
求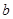 的取值范围。
的取值范围。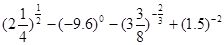 ;
;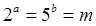 ,且
,且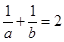 ,求
,求 的值。
的值。