题目内容
(本小题满分12分)已知函数y= cos2x+
cos2x+ sinxcosx+1,x∈R.
sinxcosx+1,x∈R.
(1)求它的振幅、周期和初相;
(2)用五点法作出它的简图;
(3)该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到的?
 cos2x+
cos2x+ sinxcosx+1,x∈R.
sinxcosx+1,x∈R.(1)求它的振幅、周期和初相;
(2)用五点法作出它的简图;
(3)该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到的?
(1)y= cos2x+
cos2x+ sinxcosx+1的振幅为A=
sinxcosx+1的振幅为A= ,周期为T=
,周期为T=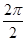 =π,初相为φ=
=π,初相为φ= .
.
(2)令x1=2x+ ,则y=
,则y= sin(2x+
sin(2x+ )+
)+ =
= sinx1+
sinx1+ ,列出下表,并描出图象如下图所示:
,列出下表,并描出图象如下图所示:
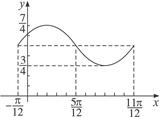
(3)方法一:将函数图象依次作如下变换:
函数y=sinx的图象 函数y=sin(x+
函数y=sin(x+ )的图象
)的图象
 函数y=sin(2x+
函数y=sin(2x+ )的图象
)的图象
 函数y=
函数y= sin(2x+
sin(2x+ )的图象
)的图象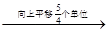 函数y=
函数y= sin(2x+
sin(2x+ )+
)+ 的图象,
的图象,
即得函数y= cos2x+
cos2x+ sinxcosx+1的图象.
sinxcosx+1的图象.
方法二:函数y=sinx的图象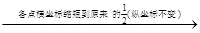 函数y=sin2x的图象
函数y=sin2x的图象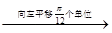 函数y=sin(2x+
函数y=sin(2x+ )的图象
)的图象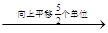 函数y=sin(2x+
函数y=sin(2x+ )+
)+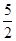 的
的
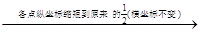 函数y=
函数y= sin(2x+
sin(2x+ )+
)+ 的图象,
的图象,
即得函数y= cos2x+
cos2x+ sinxcosx+1的图象.
sinxcosx+1的图象.
 cos2x+
cos2x+ sinxcosx+1的振幅为A=
sinxcosx+1的振幅为A= ,周期为T=
,周期为T=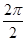 =π,初相为φ=
=π,初相为φ= .
.(2)令x1=2x+
 ,则y=
,则y= sin(2x+
sin(2x+ )+
)+ =
= sinx1+
sinx1+ ,列出下表,并描出图象如下图所示:
,列出下表,并描出图象如下图所示:| x | -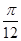 |  | 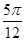 | 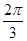 | 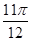 |
| x1 | 0 | 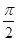 | π | 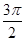 | 2π |
| y=sinx1 | 0 | 1 | 0 | -1 | 0 |
y= sin(2x+ sin(2x+ )+ )+ |  | 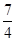 |  | 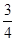 |  |

(3)方法一:将函数图象依次作如下变换:
函数y=sinx的图象
 函数y=sin(x+
函数y=sin(x+ )的图象
)的图象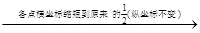 函数y=sin(2x+
函数y=sin(2x+ )的图象
)的图象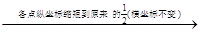 函数y=
函数y= sin(2x+
sin(2x+ )的图象
)的图象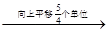 函数y=
函数y= sin(2x+
sin(2x+ )+
)+ 的图象,
的图象,即得函数y=
 cos2x+
cos2x+ sinxcosx+1的图象.
sinxcosx+1的图象.方法二:函数y=sinx的图象
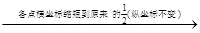 函数y=sin2x的图象
函数y=sin2x的图象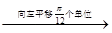 函数y=sin(2x+
函数y=sin(2x+ )的图象
)的图象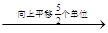 函数y=sin(2x+
函数y=sin(2x+ )+
)+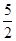 的
的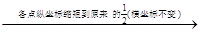 函数y=
函数y= sin(2x+
sin(2x+ )+
)+ 的图象,
的图象,即得函数y=
 cos2x+
cos2x+ sinxcosx+1的图象.
sinxcosx+1的图象.本试题主要是考查了三角函数的作图和三角函数的图像的变换的综合运用。
注意五点法作图的重要性和熟练掌握,同时对于图像的变换可以先周期再平移,也可以先平移再周期,但是平移的量不同要注意区别。
解:y= cos2x+
cos2x+ sinxcosx+1=
sinxcosx+1=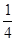 cos2x+
cos2x+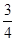 sin2x+
sin2x+
= sin(2x+
sin(2x+ )+
)+ .
.
(1)y= cos2x+
cos2x+ sinxcosx+1的振幅为A=
sinxcosx+1的振幅为A= ,周期为T=
,周期为T=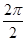 =π,初相为φ=
=π,初相为φ= .
.
(2)令x1=2x+ ,则y=
,则y= sin(2x+
sin(2x+ )+
)+ =
= sinx1+
sinx1+ ,列出下表,并描出图象如下图所示:
,列出下表,并描出图象如下图所示:
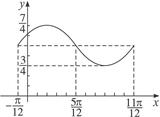
(3)方法一:将函数图象依次作如下变换:
函数y=sinx的图象 函数y=sin(x+
函数y=sin(x+ )的图象
)的图象
 函数y=sin(2x+
函数y=sin(2x+ )的图象
)的图象
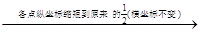 函数y=
函数y= sin(2x+
sin(2x+ )的图象
)的图象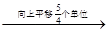 函数y=
函数y= sin(2x+
sin(2x+ )+
)+ 的图象,
的图象,
即得函数y= cos2x+
cos2x+ sinxcosx+1的图象.
sinxcosx+1的图象.
方法二:函数y=sinx的图象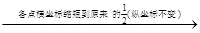 函数y=sin2x的图象
函数y=sin2x的图象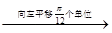 函数y=sin(2x+
函数y=sin(2x+ )的图象
)的图象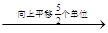 函数y=sin(2x+
函数y=sin(2x+ )+
)+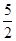 的
的
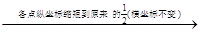 函数y=
函数y= sin(2x+
sin(2x+ )+
)+ 的图象,
的图象,
即得函数y= cos2x+
cos2x+ sinxcosx+1的图象.
sinxcosx+1的图象.
注意五点法作图的重要性和熟练掌握,同时对于图像的变换可以先周期再平移,也可以先平移再周期,但是平移的量不同要注意区别。
解:y=
 cos2x+
cos2x+ sinxcosx+1=
sinxcosx+1=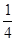 cos2x+
cos2x+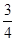 sin2x+
sin2x+
=
 sin(2x+
sin(2x+ )+
)+ .
.(1)y=
 cos2x+
cos2x+ sinxcosx+1的振幅为A=
sinxcosx+1的振幅为A= ,周期为T=
,周期为T=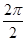 =π,初相为φ=
=π,初相为φ= .
.(2)令x1=2x+
 ,则y=
,则y= sin(2x+
sin(2x+ )+
)+ =
= sinx1+
sinx1+ ,列出下表,并描出图象如下图所示:
,列出下表,并描出图象如下图所示:| x | -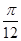 |  | 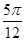 | 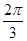 | 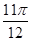 |
| x1 | 0 | 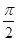 | π | 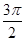 | 2π |
| y=sinx1 | 0 | 1 | 0 | -1 | 0 |
y= sin(2x+ sin(2x+ )+ )+ |  | 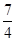 |  | 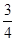 |  |

(3)方法一:将函数图象依次作如下变换:
函数y=sinx的图象
 函数y=sin(x+
函数y=sin(x+ )的图象
)的图象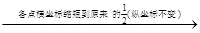 函数y=sin(2x+
函数y=sin(2x+ )的图象
)的图象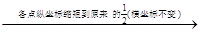 函数y=
函数y= sin(2x+
sin(2x+ )的图象
)的图象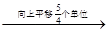 函数y=
函数y= sin(2x+
sin(2x+ )+
)+ 的图象,
的图象,即得函数y=
 cos2x+
cos2x+ sinxcosx+1的图象.
sinxcosx+1的图象.方法二:函数y=sinx的图象
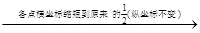 函数y=sin2x的图象
函数y=sin2x的图象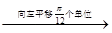 函数y=sin(2x+
函数y=sin(2x+ )的图象
)的图象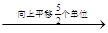 函数y=sin(2x+
函数y=sin(2x+ )+
)+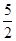 的
的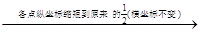 函数y=
函数y= sin(2x+
sin(2x+ )+
)+ 的图象,
的图象,即得函数y=
 cos2x+
cos2x+ sinxcosx+1的图象.
sinxcosx+1的图象.
练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 的图象与
的图象与 轴交点的纵坐标为1,在相邻的两点
轴交点的纵坐标为1,在相邻的两点 ,
, 上
上 分别取得最大值和最小值.
分别取得最大值和最小值. 的最大和最小值分别为6和2,求
的最大和最小值分别为6和2,求 的值.
的值. )图象可以看作把函数y=3sin2x的图象作下列移动而得到( )
)图象可以看作把函数y=3sin2x的图象作下列移动而得到( ) 单位
单位 的一条对称轴是( )
的一条对称轴是( )
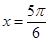


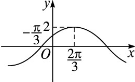
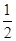 ,φ=-
,φ=-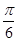
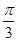
 满足
满足 ,其图象与直线
,其图象与直线 的某两个交点横坐标为
的某两个交点横坐标为 ,
, 的最小值为
的最小值为 ,则
,则  ,
,
 ,
,
 ,
, ,
, )
) , π)
, π) ,
, )
) , 2π)
, 2π) (
( ).
). 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; 
 内角
内角 的对边长分别为
的对边长分别为 ,若
,若
 且
且 试求角B和角C.
试求角B和角C.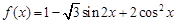 .
.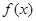 的最大值及取得最大值时的
的最大值及取得最大值时的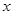 集合;
集合;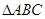 的角
的角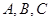 的对边分别为
的对边分别为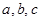 ,且
,且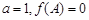 .求
.求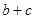 的取值范围
的取值范围