题目内容
1.已知函数f(x)=$\left\{\begin{array}{l}{1-|x-1|,x∈[0,2]}\\{\frac{1}{2}f(x-2),x∈(2,+∞)}\end{array}\right.$,若x>0,f(x)≤$\frac{k-1}{x}$恒成立,则k的取值范围[$\frac{5}{2}$,+∞).分析 作出函数f(x)的图象,利用数形结合,运用恒成立思想可得要使x>0时,f(x)≤$\frac{k-1}{x}$恒成立,则f(1)≤k-1,且f(3)≤$\frac{k-1}{3}$,f(5)≤$\frac{k-1}{5}$,f(7)≤$\frac{k-1}{7}$,…,即可得到结论.
解答 作出函数f(x)的图象如图,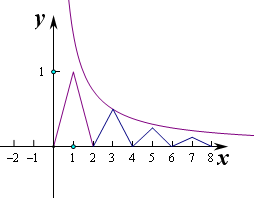
则f(1)=1,f(3)=$\frac{1}{2}$f(1),
f(5)=$\frac{1}{2}$f(3)=$\frac{1}{4}$f(1)=$\frac{1}{4}$,
f(7)=$\frac{1}{2}$f(5)=$\frac{1}{2}$×$\frac{1}{4}$=$\frac{1}{8}$,
要使x>0时,f(x)≤$\frac{k-1}{x}$恒成立,
则f(1)≤k-1,且f(3)≤$\frac{k-1}{3}$,
f(5)≤$\frac{k-1}{5}$,f(7)≤$\frac{k-1}{7}$,…,
即1≤k-1,且$\frac{1}{2}$≤$\frac{k-1}{3}$,$\frac{1}{4}$≤$\frac{k-1}{5}$,$\frac{1}{8}$≤$\frac{k-1}{7}$,…,
则$\left\{\begin{array}{l}{k-1≥1}\\{k-1≥\frac{3}{2}}\\{k-1≥\frac{5}{4}}\\{k-1≥\frac{7}{8}}\end{array}\right.$,解得k≥$\frac{5}{2}$,
即实数k的取值范围是[$\frac{5}{2}$,+∞),
故答案为:[$\frac{5}{2}$,+∞).
点评 本题主要考查不等式恒成立问题,作出函数f(x)的图象,利用数形结合是解决本题的关键.难度较大.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
| A. | [-8,-1] | B. | [-10,0] | C. | [-10,6] | D. | (-6,6] |
| A. | 命题“若a-b=1,则a2+b2>$\frac{1}{2}$”是真命题 | |
| B. | “a=b=$\frac{1}{2}$”是“$\frac{1}{a}+\frac{1}{b}$=4”的必要不充分条件 | |
| C. | 若非空集合A,B,C满足A∪B=C,且B不是A的子集,则“x∈C”是“x∈A”的充分不必要条件 | |
| D. | 命题“?x0∈R,x02+1≤2x0”的否定是“?x∈R,x2+1>2x” |
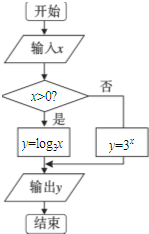
| A. | 1 | B. | 3 | C. | 9 | D. | 27 |