题目内容
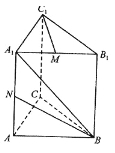
【题目】如图,直三棱柱ABC-A1B1C1底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2M,N分别是A1B1,A1A的中点。
(1)求![]() 的长度;
的长度;
(2)求cos(![]() ,
,![]() )的值;
)的值;
(3)求证:A1B⊥C1M。
【答案】(1)![]() (2)
(2)![]() (3)详见解析
(3)详见解析
【解析】
试题分析:由直三棱柱ABC-A1B1C1中,由于BCA=90°,我们可以以C为原点建立空间直角坐标系O-xyz.
(1)求出B点N点坐标,代入空间两点距离公式,即可得到答案;(2)分别求出向量![]() 的坐标,然后代入两个向量夹角余弦公式,即可得到
的坐标,然后代入两个向量夹角余弦公式,即可得到![]() 的值;(3)我们求出向量
的值;(3)我们求出向量![]() 的坐标,然后代入向量数量积公式,判定两个向量的数量积是否为0,若成立,则表明A1B⊥C1M
的坐标,然后代入向量数量积公式,判定两个向量的数量积是否为0,若成立,则表明A1B⊥C1M
试题解析:以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系。
轴建立空间直角坐标系。
(1)依题意得出![]() ;
;
(2)依题意得出![]()
![]()
∴![]() ﹤
﹤![]() ﹥=
﹥=
(3)证明:依题意将![]()
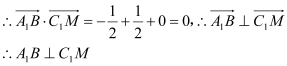

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目