题目内容
【题目】如图在正方体中![]() 中,
中,
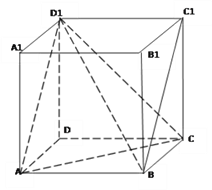
(1)求异面直线![]() 所成的角;
所成的角;
(2)求直线D1B与底面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 大小的正切值.
大小的正切值.
【答案】(1) ![]() ; (2)
; (2)![]() ; (3)
; (3)![]() .
.
【解析】试题分析:(1)连接AC,AD1,∠AD1C即为BC1与CD1所成角;
(2)DD1⊥平面ABCD,∠D1DB为直线D1B与平面ABCD所成的角;
(3)连接BD交AC于O,则DO⊥AC,∠D1OD为二面角D1﹣AC﹣D的平面角.
试题解析:
(1)连接AC,AD1,如图所示:

∵BC1∥AD1,
∴∠AD1C即为BC1与CD1所成角,
∵△AD1C为等边三角形,
∴∠AD1C=60°,
故异面直线BC1与CD1所成的角为60°;
(2)∵DD1⊥平面ABCD,
∴∠D1DB为直线D1B与平面ABCD所成的角,
在Rt△D1DB中,sin∠D1DB=![]() =
=![]()
∴直线D1B与平面ABCD所成角的正弦值为![]() ;
;
(3)连接BD交AC于O,则DO⊥AC,
根据正方体的性质,D1D⊥面AC,
∴D1D⊥AC,D1D∩DO=D,
∴AC⊥面D1OD,∴AC⊥D1O,
∴∠D1OD为二面角D1﹣AC﹣D的平面角.
设正方体棱长为1,
在直角三角形D1OD中,DO=![]() ,DD1=1,
,DD1=1,
∴tan∠D1OD=![]() .
.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目