题目内容

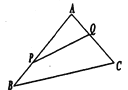
【题目】如图，某生态园将一三角形地块的一角开辟为水果园种植桃树，已知角为,的长度均大于米，现在边界处建围墙，在处围竹篱笆．

（1）若围墙总 长度为米，如何围可使得三角形地块的面积最大？

（2）已知段围墙高米，段围墙高米，造价均为每平方米元．若围围墙用了元,问如何围可使竹篱笆用料最省？

【答案】（1）当米,米时, 可使三角形地块的面积最大；（2）当米,米时, 可使篱笆最省．

【解析】

试题分析：（1）易得的面积．当且仅当时，取“”．即当米；（2）由题意得，要使竹篱笆用料最省，只需其长度最短，又

，当时, 有最小值,从而求得正解．

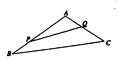
试题解析：设米，米．

（1）则的面积．

当且仅当,即时，取“”．即当米,米时, 可使三角形地块的面积最大．

（2）由题意得，即，要使竹篱笆用料最省，只需其长度最短，所以

，当时, 有最小值,此时当米,米时, 可使篱笆最省．

练习册系列答案
相关题目

【题目】在一次篮球定点投篮训练中，规定每人最多投3次，在处每投进一球得3分；在处每投进一球得2分，如果前两次得分之和超过3分就停止投篮；否则投第3次，某同学在处的抽中率，在处的抽中率为，该同学选择现在处投第一球，以后都在处投，且每次投篮都互不影响，用表示该同学投篮训练结束后所得的总分，其分布列为：

0

2

3

4

5

0.03

（1）求的值；

（2）求随机变量的数学期望；

（3）试比较该同学选择上述方式投篮得分超过3分与选择都在处投篮得分超过3分的概率的大小．

【题目】如图，在四棱锥中，平面，四边形为正方形，点分别为线段上的点，．

（1）求证：平面平面；

（2）求证：当点不与点重合时，平面；

（3）当，时，求点到直线距离的最小值．

【题目】已知为坐标原点，椭圆：的左、右焦点分别为，右顶点为,上顶点为, 若成等比数列，椭圆上的点到焦点的最短距离为．

（1）求椭圆的标准方程；

（2）设为直线上任意一点，过的直线交椭圆于点，且，求的最小值．

【题目】一青蛙从点开始依次水平向右和竖直向上跳动，其落点坐标依次是，（如图所示，坐标以已知条件为准），表示青蛙从点到点所经过的路程．

（1）若点为抛物线（）准线上一点，点均在该抛物线上，并且直线经过该抛物线的焦点，证明．

（2）若点要么落在所表示的曲线上，要么落在所表示的曲线上，并且,试写出（不需证明）；

（3）若点要么落在所表示的曲线上，要么落在所表示的曲线上，并且，求的表达式．

【题目】如图，在四面体ABCD中，截面PQMN是正方形，则下列命题中，正确的为________ (填序号)．

①AC⊥BD；②AC∥截面PQMN；③AC＝BD；④异面直线PM与BD所成的角为45°.

【题目】如图在正方体中中，

（1）求异面直线所成的角；

（2）求直线D1B与底面所成角的正弦值；

（3）求二面角大小的正切值.

【题目】已知椭圆的离心率为，点在椭圆上．

（I）求椭圆的方程；

（II）设动直线与椭圆有且仅有一个公共点，判断是否存在以原点为圆心的圆，满足此圆与相交于两点（两点均不在坐标轴上），且使得直线的斜率之积为定值？若存在，求此圆的方程；若不存在，说明理由．

【题目】公司从某大学招收毕业生，经过综合测试，录用了名男生和名女生，这名毕业生的测试成绩如茎叶图所示（单位：分），公司规定：成绩在分以上者到甲部门工作；分以下者到乙部门工作，另外只有成绩高于分才能担任助理工作。

（1）如果用分层抽样的方法从甲部门人选和乙部门人选中选取人，再从这人中选人，那么至少有一人是甲部门人选的概率是多少？

（2）若从所有甲部门人选中随机选人，用表示所选人员中能担任助理工作的男生人数，写出的分布列，并求出的数学期望.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网