题目内容
某企业生产一种产品时,固定成本为5000元,而每生产100台产品时直接消耗成本要增加2500元,市场对此商品年需求量为500台,销售的收入函数为R(x)=5x-x2(万元)(0≤x≤5),其中x是产品售出的数量(单位:百台)
(1)把利润表示为年产量的函数;
(2)年产量多少时,企业所得的利润最大?
(3)年产量多少时,企业才不亏本?
(1)利润y是指生产数量x的产品售出后的总收入R(x)与其总成本C(x)之差,由题意,当x≤5时,产品能全部售出,当x>5时,只能销售500台,所以
y=
=.
(2)在0≤x≤5时,y=-x2+4.75x-0.5,
当x=-=4.75(百台)时,ymax=10.78125(万元);
当x>5(百台)时,y<12-0.25×5=10.75(万元),
所以当生产475台时,利润最大.
(3)要使企业不亏本,即要求
或,
解得5≥x≥4.75-≈0.1(百台)或5<x<48(百台)时,即企业年产量在10台到4800台之间时,企业不亏本.
解析

练习册系列答案
相关题目
 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个不同的交点. 经过这三个交点的圆记为
的图象与两坐标轴有三个不同的交点. 经过这三个交点的圆记为 .
. 的取值范围;
的取值范围;
 (
( )的图象与反比例函数
)的图象与反比例函数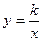 图象相交于点
图象相交于点 ,已知点
,已知点 的坐标为
的坐标为 ,点
,点 在第三象限内,且
在第三象限内,且 的面积为
的面积为 (
( 为坐标原点)
为坐标原点)
 的值;
的值; 轴的另一个交点为
轴的另一个交点为 ,
, 点为线段
点为线段

 (
( ∈R).
∈R). 上具有单调性,求
上具有单调性,求 ,对任意实数
,对任意实数 ,有
,有 恒成立;数列
恒成立;数列 满足
满足 .
. 的解析式和值域;
的解析式和值域; ,使得当
,使得当 时,数列
时,数列 ,是否存在非零整数
,是否存在非零整数 ,使得对任意
,使得对任意 ,都有
,都有
 恒成立,若存在,
恒成立,若存在,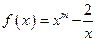 ,且
,且 。
。 的值;
的值; 的奇偶性;
的奇偶性; 上的单调性,并给予证明。
上的单调性,并给予证明。