Question

定义max{a，b}=

a(a≥b) b(a＜b)

设实数x、y满足约束条件

|x|≤2 |y|≤2

且z=max{4x+y，3x-y}，则z的取值范围为（　　）．

• A、[-6，0]
• B、[-7，10]
• C、[-6，8]
• D、[-7，8]

Answer 1

分析：本题属于线性规划问题，先找出可行域，即四边形ABCD上及其内部，（4x+y）与（3x-y）相等的分界线x+2y=0，令z₁=4x+y，点（x，y）在四边形ABCD上及其内部，求得z_1范围；令z₂=3x-y，点（x，y）在四边形ABEF上及其内部（除AB边）求得z₂范围，
将这2个范围取并集可得答案．

解答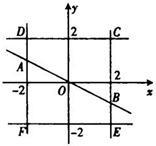：解：∵（4x+y）-（3x-y）=x+2y，
∴z=

4x+y (x+2y≥0) 3x-y (x+2y＜0)

直线x+2y=0
将约束条件

|x|≤2 |y|≤2

所确定的平面区域分为两部分．如图，
令z₁=4x+y，点（x，y）在四边形ABCD上及其内部，求得-7≤z₁≤10；
令z₂=3x-y，点（x，y）在四边形ABEF上及其内部（除AB边），
求得-7≤z₂≤8．综上可知，z的取值范围为[-7，10]．
故选B．

点评：表面上看约束条件和目标函数都是静态的，实际上二者都是动态变化的，目标函数是z=4x+y还是z=3x-y并没有明确确定下来，直线x+2y=0又将原可行域分为两部分．本题看似风平浪静，实际暗藏玄机，化动为静，在静态状态下，从容破解问题．