Question

定义max{a，b}=

a，a≥b b，a＜b

，设实数x，y满足约束条件

|x|≤2 |y|≤2

，z=max{2x-y，3x+y}，则z的取值范围是（　　）

A．[-5，6]

B．[-3，6]

C．[-5，8]

D．[-8，8]

Answer 1

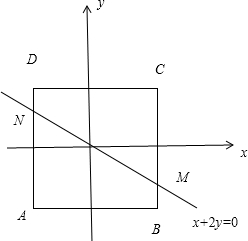
分析：由题意可得约束条件所满足的可行域如图所示的正方形ABCD，由Z=

2x-y，x+2y≤0 3x+y，x+2y＞0

当x+2y＜0时的可行域即为图中的四边形ABMN，Z=2x-y在N（-2，1）处取得最小值-5，在B（2，-2）处取得最大值6；当x+2y≥0时的可行域为图中的四边形MCDN，Z=3x+y在C（2，2）处取得最小值8，从而可求Z的取值范围

解答：解：由题意可得约束条件所满足的可行域如图所示的正方形ABCD
由Z=

2x-y，x+2y≤0 3x+y，x+2y＞0

当x+2y＜0时的可行域即为图中的四边形ABMN，Z=2x-y在N（-2，1）处取得最小值-5，在B（2，-2）处取得最大值6
当x+2y≥0时的可行域为图中的四边形MCDN，Z=3x+y在C（2，2）处取得最小值8
∴-5≤Z≤8
故选：C

点评：本题主要考查了简单的线性规划，解题的关键是要根据题目中的定义确定目标函数及可行域的条件以及，属于知识的综合应用题．