题目内容
下列说法正确的是
①若集合A={y|y=x-1},B={y|y=x2-1},则A∩B={(0,-1),(1,0)};
②函数y=f(x)的图象与x=a(a∈R)的交点个数只能为0或1;
③f(x)=lg(x+
)是定义在R上的奇函数;
④若函数f(x)在(-∞,0],(0,+∞)都是单调增函数,则f(x)在(-∞,+∞)上也是增函数;
⑤定义max(a,b)=
,则f(x)=max(x+1,4-2x)的最小值为2.
②③⑤
②③⑤
.(只填正确说法序号)①若集合A={y|y=x-1},B={y|y=x2-1},则A∩B={(0,-1),(1,0)};
②函数y=f(x)的图象与x=a(a∈R)的交点个数只能为0或1;
③f(x)=lg(x+
| x2+1 |
④若函数f(x)在(-∞,0],(0,+∞)都是单调增函数,则f(x)在(-∞,+∞)上也是增函数;
⑤定义max(a,b)=
|
分析:①根据集合的定义和运算进行判断.②根据函数的定义进行判断.③根据函数奇偶性的定义和对数的运算判断.④根据函数单调性的定义进行判断.⑤根据条件定义进行判断.
解答:解:①∵A={y|y=x-1}={y|y∈R},B={y|y=x2-1}={y|y≥-1},∴A∩B={y|y≥-1},∴①错误.
②根据函数的定义可知,当x=a为定义域内的一个值时,此时y=f(x)的图象与x=a(a∈R)的交点个数为1个,
当x=a不是定义域内的值时,y=f(x)的图象与x=a(a∈R)的交点个数为0,∴②正确.
③f(x)的定义域为R,f(-x)+f(x)=lg(-x+
)+lg?(x+
)=lg?[(-x+
)(x+
)]=lg?[(
)2-x2]=lg?1=0,
∴f(-x)=-f(x),即函数f(x)为奇函数,∴③正确.
④比如函数f(x)=
,满足f(x)在(-∞,0],(0,+∞)都是单调增函数,但在(-∞,+∞)上不是单调函数,∴④错误.
⑤根据定义,作出函数y=x+1和y=4-2x的图象如图:
由x+1=4-2x,解得x=1,此时y=1+1=2,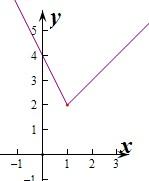
∴当x=1时有最小值y=2,即f(x)=max(x+1,4-2x)的最小值为2,正确.
故正确的是:②③⑤.
故答案为:②③⑤.
②根据函数的定义可知,当x=a为定义域内的一个值时,此时y=f(x)的图象与x=a(a∈R)的交点个数为1个,
当x=a不是定义域内的值时,y=f(x)的图象与x=a(a∈R)的交点个数为0,∴②正确.
③f(x)的定义域为R,f(-x)+f(x)=lg(-x+
| x2+1 |
| x2+1 |
| x2+1 |
| x2+1 |
| x2+1 |
∴f(-x)=-f(x),即函数f(x)为奇函数,∴③正确.
④比如函数f(x)=
|
⑤根据定义,作出函数y=x+1和y=4-2x的图象如图:
由x+1=4-2x,解得x=1,此时y=1+1=2,

∴当x=1时有最小值y=2,即f(x)=max(x+1,4-2x)的最小值为2,正确.
故正确的是:②③⑤.
故答案为:②③⑤.
点评:本题主要考查了与函数有关的命题的真假判断,要求熟练掌握函数的有关性质.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目