题目内容
【题目】已知椭圆C： 
+ 
=1（a＞b＞0）的离心率为 
，且经过点M（﹣3，﹣1）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线l：x﹣y﹣2=0与椭圆C交于A，B两点，点P为椭圆C上一动点，当△PAB的面积最大时，求点P的坐标及△PAB的最大面积．
【答案】解：（Ⅰ）∵椭圆C： 
+ 
=1（a＞b＞0）的离心率为 
，且经过点M（﹣3，﹣1），
∴ 
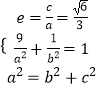，解得a2=12，b2=4，
∴椭圆C的方程为 
．
（Ⅱ）将直线x﹣y﹣2=0代入 中，消去y得，x2﹣3x=0．
解得x=0或x=3．…（5分）
∴点A（0，﹣2），B（3，1），∴|AB|= 
=3 
．
在椭圆C上求一点P，使△PAB的面积最大，则点P到直线l的距离最大．
设过点P且与直线l平行的直线方程为y=x+b．
将y=x+b代入 ，整理得4x2+6bx+3（b2﹣4）=0．
令△=（6b）2﹣4×4×3（b2﹣4）=0，解得b=±4．
将b=±4代入方程4x2+6bx+3（b2﹣4）=0，解得x=±3．
由题意知当点P的坐标为（﹣3，1）时，△PAB的面积最大．
且点P（﹣3，1）到直线l的距离为d= 
=3 ．
△PAB的最大面积为S= 
=9．
【解析】（Ⅰ）利用椭圆的离心率为 ，且经过点M（﹣3，﹣1），列出方程组，求出a，b，由此能求出椭圆C的方程．（Ⅱ）将直线x﹣y﹣2=0代入 中，得，x2﹣3x=0．求出点A（0，﹣2），B（3，1），从而|AB|=3 ，在椭圆C上求一点P，使△PAB的面积最大，则点P到直线l的距离最大．设过点P且与直线l平行的直线方程为y=x+b．将y=x+b代入 ，得4x2+6bx+3（b2﹣4）=0，由根的判别式求出点P（﹣3，1）时，△PAB的面积最大，由此能求出△PAB的最大面积．
名校课堂系列答案
