题目内容
5.已知α∈(0,$\frac{π}{2}$),β∈($\frac{π}{2}$,π),cosα=$\frac{1}{3}$,cos(α+β)=-$\frac{4}{5}$,则cosβ=$\frac{-4-6\sqrt{2}}{15}$.分析 有条件利用同角三角函数的基本关系求得sinα、sin (α+β)的值,再利用两角和差的三角公式求得 cosβ=cos[(α+β)-α]的值.
解答 解:∵α∈(0,$\frac{π}{2}$),β∈($\frac{π}{2}$,π),∴α+β∈($\frac{π}{2}$,$\frac{3π}{2}$).
∵cosα=$\frac{1}{3}$∈(0,$\frac{1}{2}$),∴sinα=$\sqrt{{1-cos}^{2}α}$=$\frac{2\sqrt{2}}{3}$,α∈($\frac{π}{3}$,$\frac{π}{2}$),α+β∈($\frac{5π}{6}$,$\frac{3π}{2}$).
∵cos(α+β)=-$\frac{4}{5}$∈(-$\frac{\sqrt{3}}{2}$,-$\frac{\sqrt{2}}{2}$),∴α+β∈($\frac{7π}{6}$,$\frac{5π}{4}$),
∴sin (α+β)=-$\sqrt{{1-cos}^{2}(α+β)}$=-$\frac{3}{5}$,
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=-$\frac{4}{5}$×$\frac{1}{3}$+(-$\frac{3}{5}$)×$\frac{2\sqrt{2}}{3}$=$\frac{-4-6\sqrt{2}}{15}$,
故答案为:$\frac{-4-6\sqrt{2}}{15}$.
点评 本题主要考查同角三角函数的基本关系、两角和差的三角公式的应用,属于中档题.

练习册系列答案
相关题目
20.已知点M是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)左支上一点,F是其右焦点,若$\overrightarrow{OP}$•$\overrightarrow{MF}$=0,且$\overrightarrow{PM}$=-$\frac{1}{2}$$\overrightarrow{MF}$,当|$\overrightarrow{OP}$|=$\frac{1}{2}$a时,该双曲线的离心率为( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\sqrt{10}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
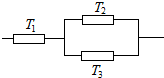 三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2}$,$\frac{3}{4}$,$\frac{3}{4}$,且是互相独立的.将它们中某两个元件并联后再和第三元件串联接入电路,在如图的电路中,电路不发生故障的概率是$\frac{15}{32}$.
三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2}$,$\frac{3}{4}$,$\frac{3}{4}$,且是互相独立的.将它们中某两个元件并联后再和第三元件串联接入电路,在如图的电路中,电路不发生故障的概率是$\frac{15}{32}$.