题目内容
【题目】长方体ABCD﹣A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点.
(1)求证:BD1∥平面A1DE;
(2)求证:A1D⊥平面ABD1 . 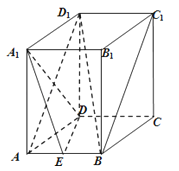
【答案】证明:(1)连结A1D,AD1 , A1D∩AD1=O,连结OE,
∵长方体ABCD﹣A1B1C1D1中,ADD1A1是矩形,
∴O是AD1的中点,∴OE∥BD1 ,
∵OE∥BD1 , OE平面ABD1 , BD1平面ABD1 ,
∴BD1∥平面A1DE.
(2)∵长方体ABCD﹣A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点,
∴ADD1A1是正方形,∴A1D⊥AD1 ,
∵长方体ABCD﹣A1B1C1D1中,AB⊥平面ADD1A1 ,
∴A1D⊥AB,
又AB∩AD1=A,∴A1D⊥平面ABD1 . 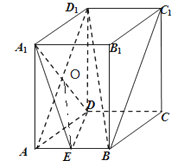
【解析】(1)连结A1D,AD1 , A1D∩AD1=O,连结OE,推导出OE∥BD1 , 由此能证明BD1∥平面A1DE.
(2)推导出A1D⊥AD1 , A1D⊥AB,由此能证明A1D⊥平面ABD1 .

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目