题目内容
设函数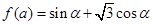 ,其中,角
,其中,角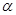 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与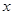 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点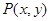 ,且
,且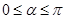 .
.
(1)若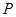 点的坐标为(-
点的坐标为(-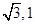 ),求
),求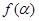 的值;
的值;
(2)若点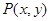 为平面区域
为平面区域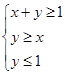 上的一个动点,试确定角
上的一个动点,试确定角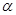 的取值范围,并求函数
的取值范围,并求函数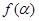 的值域.
的值域.
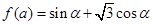 ,其中,角
,其中,角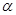 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与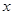 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点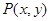 ,且
,且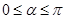 .
.(1)若
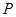 点的坐标为(-
点的坐标为(-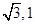 ),求
),求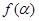 的值;
的值;(2)若点
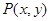 为平面区域
为平面区域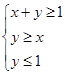 上的一个动点,试确定角
上的一个动点,试确定角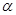 的取值范围,并求函数
的取值范围,并求函数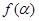 的值域.
的值域.(1)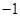 ;(2)
;(2)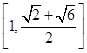 .
.
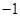 ;(2)
;(2)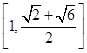 .
.试题分析:(1)由三角函数的定义求解
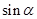 与
与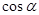 ,进而求
,进而求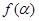 的值;(2)由平面区域
的值;(2)由平面区域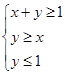 的可行域可得角
的可行域可得角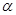 的范围,再求解
的范围,再求解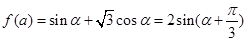 的值域,本题将三角化简求值与线性规划知识联系在一起,具有新颖性.
的值域,本题将三角化简求值与线性规划知识联系在一起,具有新颖性.试题解析:(1)由三角函数的定义,得
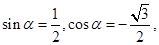
故
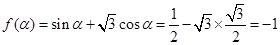 4分
4分(2)作出平面区域
 (即三角形区域ABC)如图所示,
(即三角形区域ABC)如图所示,其中
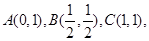 于是
于是 7分
7分又
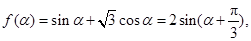 且
且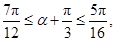
故当
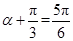 ,即
,即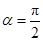 时,
时,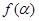 取得最小值,且最小值为1.
取得最小值,且最小值为1.当
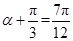 ,即
,即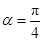 时,
时,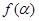 取得最大值,且最大值为
取得最大值,且最大值为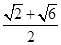 .
.故函数
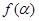 的值域为
的值域为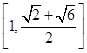 . 12分
. 12分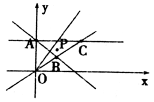

练习册系列答案
相关题目
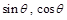 是关于
是关于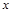 的方程
的方程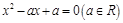 的两个根.
的两个根.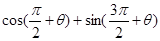 的值;
的值;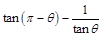 的值.
的值.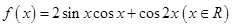 .
.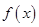 的最小正周期和最大值;
的最小正周期和最大值;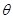 为锐角,且
为锐角,且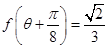 ,求
,求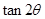 的值.
的值.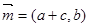 ,
,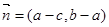 ,且
,且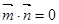 ,其中A、B、C是
,其中A、B、C是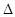 ABC的内角,
ABC的内角,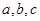 分别是角A,B,C的对边。
分别是角A,B,C的对边。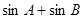 的取值范围;
的取值范围;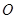 为坐标原点,向量
为坐标原点,向量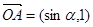 ,
,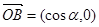 ,
,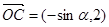 ,点
,点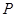 满足
满足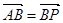 .
.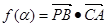 ,
,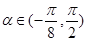 ,讨论函数
,讨论函数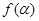 的单调性,并求其值域;
的单调性,并求其值域;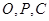 三点共线,求
三点共线,求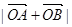 的值.
的值.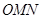 是半径为2,圆心角为
是半径为2,圆心角为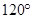 的扇形,
的扇形,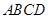 是扇形的内接矩形.
是扇形的内接矩形.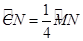 时,求
时,求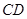 的长;
的长;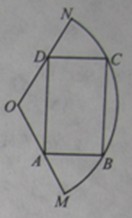
 为第二象限角,
为第二象限角, ,则
,则 ( )
( )



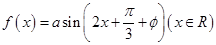 为偶函数,则
为偶函数,则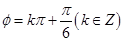 ;
;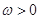 ,函数
,函数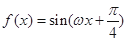 在
在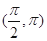 上单调递减,则
上单调递减,则 的取值范围是
的取值范围是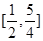 ;
;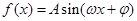 (其中
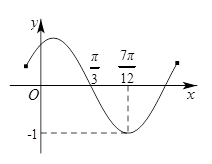
(其中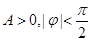 )的图象如图所示,则
)的图象如图所示,则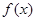 的解析式为
的解析式为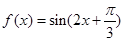 ;
;
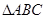 的内角
的内角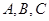 所对的边为
所对的边为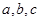 若
若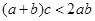 ,则
,则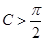 ;
;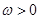 ,函数
,函数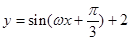 的图象向右平移
的图象向右平移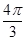 个单位后与原图象重合,则
个单位后与原图象重合,则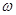 的最小值是
的最小值是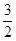 .
. ,
, ,则
,则 的值为________.
的值为________.