Question

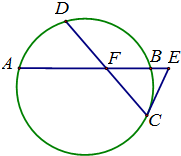（2013•顺义区二模）如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF=CF=

2

，AF=2BF，若CE与圆相切，且CE=

7

2

，则BE=

1

2

．

Answer 1

分析：利用相交弦定理可得BF•AF=DF•FC，解出BF；再利用切割线定理可得CE²=BE•EA，解得BE．

解答：解：由相交弦定理得BF•AF=DF•FC，
∵DF=CF=

2

，AF=2BF，
∴2BF2=(

2

)2，解得BF=1，∴AF=2．
∵CE与圆相切，
∴由切割线定理可得CE²=BE•EA，
∴(

7

2

)2=BE•(BE+1+2)，∵BE＞0，解得BE=

1

2

．
故答案为

1

2

．

点评：熟练掌握相交弦定理和切割线定理是解题的关键．