题目内容
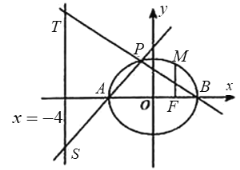
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是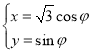 (
(![]() 为参数,
为参数,![]() ),在以坐标原点为极点,
),在以坐标原点为极点,![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,等边
,等边![]() 的顶点都在
的顶点都在![]() 上,且点
上,且点![]() ,
,![]() ,
,![]() 按照逆时针方向排列,点
按照逆时针方向排列,点![]() 的极坐标为
的极坐标为![]() .
.
(Ⅰ)求点![]() ,
,![]() ,
,![]() 的直角坐标;
的直角坐标;
(Ⅱ)设![]() 为
为![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的距离的取值范围.
的距离的取值范围.
【答案】(Ⅰ)![]() 点的直角坐标为
点的直角坐标为![]() ,
,![]() 点的直角坐标为
点的直角坐标为![]() ,
,![]() 点的直角坐标为
点的直角坐标为![]() .
.
(Ⅱ)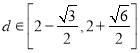
【解析】
(Ⅰ)由点![]() 的极坐标和
的极坐标和![]() ,
,![]() ,
,![]() 的排列顺序,得到点
的排列顺序,得到点![]() 和点
和点![]() 的极坐标,再由
的极坐标,再由![]() 求出
求出![]() ,
,![]() ,
,![]() 的直角坐标即可;
的直角坐标即可;
(Ⅱ)由点![]() 和点
和点![]() 的坐标可得直线
的坐标可得直线![]() 的方程
的方程![]() ,设点
,设点![]() ,由点到直线距离公式表示出点
,由点到直线距离公式表示出点![]() 到直线
到直线![]() 的距离
的距离![]() ,再由辅助角公式和三角函数的性质得到
,再由辅助角公式和三角函数的性质得到![]() 的取值范围即可.
的取值范围即可.
(Ⅰ)由题意,等边![]() 的顶点都在
的顶点都在![]() 上,
上,
且点![]() ,
,![]() ,
,![]() 按照逆时针方向排列,点
按照逆时针方向排列,点![]() 的极坐标为
的极坐标为![]() ,
,
所以点![]() 的极坐标
的极坐标![]() ,点
,点![]() 的极坐标
的极坐标![]() ,
,
由![]() ,
,
可得![]() 点的直角坐标为
点的直角坐标为![]() ,
,
![]() 点的直角坐标为
点的直角坐标为![]() ,
,
![]() 点的直角坐标为
点的直角坐标为![]() .
.
(Ⅱ)由(Ⅰ)知,![]() ,
,![]() ,
,
所以得![]() 的直线方程为:
的直线方程为:![]() ,
,
设点![]() ,
,
则点![]() 到直线
到直线![]() 的距离
的距离![]() 为
为
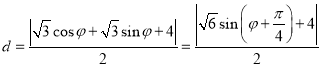 ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
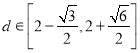 .
.

练习册系列答案
相关题目
【题目】疫情爆发以来,相关疫苗企业发挥专业优势与技术优势争分夺秒开展疫苗研发.为测试疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),选定2000个样本分成三组,测试结果如“下表:
|
|
| |
疫苗有效 | 673 |
|
|
疫苗无效 | 77 | 90 |
|
已知在全体样本中随机抽取1个,抽到![]() 组疫苗有效的概率是0.33.
组疫苗有效的概率是0.33.
(1)求![]() ,
,![]() 的值;
的值;
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,求![]() 组应抽取多少个?
组应抽取多少个?
(3)已知![]() ,
,![]() ,求疫苗能通过测试的概率.
,求疫苗能通过测试的概率.