题目内容
【题目】已知函数![]() .
.
(1)若f(x)<2x在(1,+∞)上恒成立,求实数a的取值范围;
(2)若函数y=f(x)在[m,n]上的值域是[m,n],求实数a的取值范围.
【答案】(1)a≤3 (2)a∈{0}∪(2,+∞)
【解析】
(1)利用分离参数法将不等式转化为a<![]() +2x,求出
+2x,求出![]() +2x的最小值即可求解.
+2x的最小值即可求解.
(2)讨论![]() 的正负,利用函数的单调性解方程组即可求解.
的正负,利用函数的单调性解方程组即可求解.
(1)若f(x)<2x在(1,+∞)上恒成立,
得a﹣![]() <2x即a<
<2x即a<![]() +2x,
+2x,
记g(x)=![]() +2x,在(1,+∞)上是增函数,
+2x,在(1,+∞)上是增函数,
得g(x)>g(1)=3,
所以:a≤3
(2)函数y=f(x)的定义域为(﹣∞,0)∪(0,+∞)
(ⅰ)当n>m>0时,f(x)在[m,n]上是增函数,
故![]() ,即
,即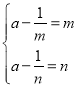 ,
,
所以方程![]() 中
中![]() 有两解,
有两解,![]() a>2;
a>2;
(ⅱ) 当0>n>m时,f(x)在[m,n]上是减函数,
故![]() ,即
,即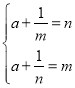 ,两式作差且
,两式作差且![]() 可得
可得![]() ,
,
此时解得:a=0;
所以:a∈{0}∪(2,+∞).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目