题目内容
设 ,函数
,函数 .
.
(Ⅰ)求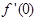 的值;
的值;
(Ⅱ)求函数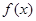 的单调区间.
的单调区间.
 ,函数
,函数 .
.(Ⅰ)求
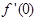 的值;
的值;(Ⅱ)求函数
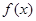 的单调区间.
的单调区间.(Ⅰ) ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.试题分析:(Ⅰ)本小题首先需要对原函数求导得
 ,然后代入
,然后代入 ;
;(Ⅱ)本小题首先令
 ,得
,得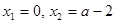 ,然后分析二根之间的关系,需要分类讨论,按
,然后分析二根之间的关系,需要分类讨论,按 ;
; ;
; 进行.
进行.试题解析:(Ⅰ)
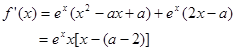
∴
 . 3分
. 3分(Ⅱ)令
 ,得
,得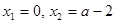 4分
4分函数
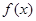 定义域为R,且对任意
定义域为R,且对任意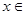 R,
R, ,
,当
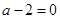 ,即
,即 时,
时,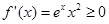 ,
,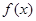 的单调递增区间是
的单调递增区间是 . 6分
. 6分当
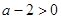 ,即
,即 时,
时, | 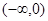 | 0 |  |  |  |
 | + | 0 | - | 0 | + |
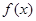 | ↗ | | ↘ | | ↗ |
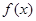 的单调递增区间是
的单调递增区间是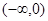 ,
, ,单调递减区间是
,单调递减区间是 . 9分
. 9分当
 ,即
,即 时,
时, | 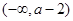 |  | 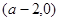 | 0 |  |
 | + | 0 | - | 0 | + |
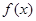 | ↗ | | ↘ | | ↗ |
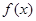 的单调递增区间是
的单调递增区间是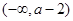 ,
, ,单调递减区间是
,单调递减区间是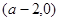 . 12分
. 12分综上,
 时,
时,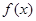 的单调递增区间是
的单调递增区间是 .
.  时,
时,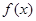 的单调递增区间是
的单调递增区间是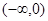 ,
, ,
,单调递减区间是
 .
. 时,
时,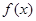 的单调递增区间是
的单调递增区间是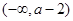 ,
, ,
,单调递减区间是
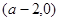 . 13分
. 13分
练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
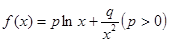 ,若
,若 时,
时, 有极小值
有极小值 ,
,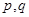 的取值;
的取值; 中,
中,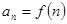 ,求证:数列
,求证:数列 项和
项和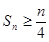 ;
; ,若
,若 有极值且极值为
有极值且极值为 ,则
,则 是否具有确定的大小关系?证明你的结论.
是否具有确定的大小关系?证明你的结论. ,
,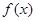 的单调区间;
的单调区间;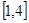 内的最小值为
内的最小值为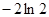 ,求
,求 的值.(参考数据
的值.(参考数据 )
) 元/本(9≤
元/本(9≤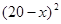 万本.
万本. (万元)与每本书的定价
(万元)与每本书的定价 .
.
 时,求函数
时,求函数 的单调区间;
的单调区间; ,试问函数
,试问函数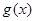 在
在 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由. ,
, .
. ,
,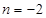 时,求
时,求 的单调区间;
的单调区间;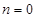 ,且
,且 时,求
时,求 上的最大值.
上的最大值.
 在区间
在区间 上是增函数,则实数
上是增函数,则实数 的取值范围是 .
的取值范围是 . 在(0, 1)上不是单调函数,则实数
在(0, 1)上不是单调函数,则实数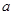 的取值范围为 _____.
的取值范围为 _____.