题目内容
【题目】如图所示,将一块直角三角形板![]() 置于平面直角坐标系中,已知
置于平面直角坐标系中,已知![]() ,点
,点![]() 是三角板内一点,现因三角板中,阴影部分受到损坏,要把损坏部分锯掉,可用经过点
是三角板内一点,现因三角板中,阴影部分受到损坏,要把损坏部分锯掉,可用经过点![]() 的任一直线
的任一直线![]() 将三角板锯成
将三角板锯成![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() .
.
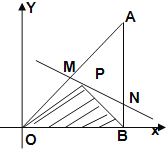
(1)用![]() 表示出直线
表示出直线![]() 的方程,并求出点
的方程,并求出点![]() 的坐标;
的坐标;
(2)求出![]() 的取值范围及其所对应的倾斜角
的取值范围及其所对应的倾斜角![]() 的范围;
的范围;
(3)求![]() 面积的取值范围.
面积的取值范围.
【答案】(1)MN方程为:![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]()
【解析】
(1)先利用点斜式得出直线![]() 的方程,再得直线OA方程为:y=x ,直线AB方程为:x=1,分别与直线MN的方程联立即可得出;
的方程,再得直线OA方程为:y=x ,直线AB方程为:x=1,分别与直线MN的方程联立即可得出;
(2)
(3)利用三角形的面积计算公式可得S△AMN,通过换元利用导数即可得出其单调性最值,进而得出区间D;
(1)依题意,得MN方程为:![]() ,即
,即![]() ,
,
∵AB⊥OB,|AB|=|OB|=1,∴直线OA方程为:y=x ,直线AB方程为:x=1,
联立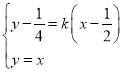 ,得
,得![]() .
.
联立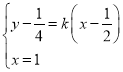 ,得
,得![]() .
.
(2)由(1)知:![]() ,∴k>1或k≤
,∴k>1或k≤![]() ,且
,且![]() ,得k≥
,得k≥![]() ,∴
,∴![]() .
.
∵直线的倾斜角![]() ,且
,且![]() ,∴
,∴![]() .
.
(3)在![]() 中,由(2)知:
中,由(2)知:
S△AMN=![]() =
=![]() .
.
设![]() ,设
,设![]() .∵
.∵![]() ,
,
∴f(t)在![]() 是单调递增.∴当
是单调递增.∴当![]() 时,
时,![]() ,即当1﹣k=
,即当1﹣k=![]() 时即k=
时即k=![]() 时,(S△)max=
时,(S△)max=![]()
当![]() 时,
时,![]() ,即当1﹣k=
,即当1﹣k=![]() 时即k=
时即k=![]() 时,(S△)min=
时,(S△)min=![]() ,
,
![]() 面积的取值范围
面积的取值范围![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目