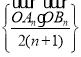题目内容
【题目】已知复数 z a bi ，其中 a .b 为实数，i 为虚数单位， 
为 z 的共轭复数，且存在非零实数 t ，使
成立.
（1）求 2a b 的值；
（2）若| z 2 | 5，求实数 a 的取值范围.
【答案】（1）6；（2）
【解析】
（1）由题意可得，
，所以
，由此能求出2a+b的值．
（2）由|z﹣2|≤5得
，由b＝6﹣2a，得（a﹣2）2+（6﹣2a）2≤25，由此能求出a的取值范围．
解：（1）由题意可得，，
所以，
由①得，
，
代入②得
，
所以2a+b＝6．
（2）由|z﹣2|≤5，
得|（a﹣2）+bi|≤5，
即，
由（1）得b＝6﹣2a，
所以（a﹣2）2+（6﹣2a）2≤25，
化简得5a2﹣28a+15≤0，
所以a的取值范围是
．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
