题目内容
.椭圆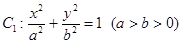 的左准线为
的左准线为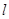 ,左、右焦点分别为
,左、右焦点分别为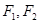 ,抛物线
,抛物线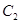 的准线也为
的准线也为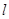 ,焦点为
,焦点为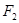 ,记
,记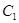 与
与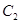 的一个交点为
的一个交点为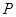 ,则
,则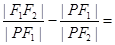 ( )
( )
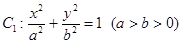 的左准线为
的左准线为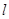 ,左、右焦点分别为
,左、右焦点分别为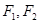 ,抛物线
,抛物线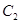 的准线也为
的准线也为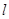 ,焦点为
,焦点为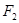 ,记
,记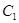 与
与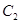 的一个交点为
的一个交点为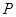 ,则
,则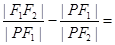 ( )
( )A.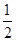 | B.1 | C.2 | D.与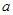 , ,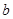 的取值有关 的取值有关 |
B
P到椭圆的左准线的距离设为d,先利用椭圆的第二定义求得|PF1|=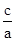 d,利用抛物线的定义可知|PF2|=d,最后根据椭圆的定义可知|PF2|+|PF1|=2a且
d,利用抛物线的定义可知|PF2|=d,最后根据椭圆的定义可知|PF2|+|PF1|=2a且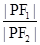 =
=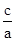 ,求得|PF2|,|PF1|,可得
,求得|PF2|,|PF1|,可得
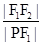 -
-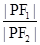 .
.
解:椭圆的离心率为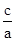 ,
,
P到椭圆的左准线的距离设为d,
则|PF1|=1/2d,|PF2|+|PF1|=2a,又|PF2|=d,
∴d=|PF2|=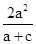 ,|PF1|=
,|PF1|=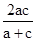 .
.
得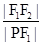 -
-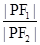 =
=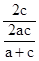 -
-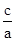 =1.
=1.
故选B.
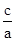 d,利用抛物线的定义可知|PF2|=d,最后根据椭圆的定义可知|PF2|+|PF1|=2a且
d,利用抛物线的定义可知|PF2|=d,最后根据椭圆的定义可知|PF2|+|PF1|=2a且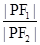 =
=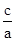 ,求得|PF2|,|PF1|,可得
,求得|PF2|,|PF1|,可得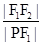 -
-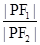 .
.解:椭圆的离心率为
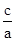 ,
,P到椭圆的左准线的距离设为d,
则|PF1|=1/2d,|PF2|+|PF1|=2a,又|PF2|=d,
∴d=|PF2|=
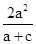 ,|PF1|=
,|PF1|=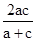 .
.得
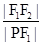 -
-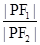 =
=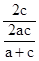 -
-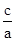 =1.
=1.故选B.

练习册系列答案
相关题目
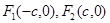 是椭圆
是椭圆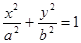
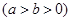 的两个焦点,
的两个焦点,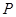 是以
是以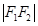 为直径的圆与椭圆的一个交点,且
为直径的圆与椭圆的一个交点,且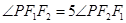 ,则该椭圆的离心率为 ( )
,则该椭圆的离心率为 ( )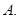 .
.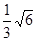
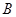 .
.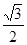
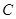 .
.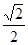
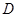 .
.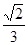
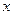 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为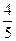 ,且过点
,且过点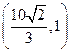 (题干自编)
(题干自编) 分别切椭圆C与圆
分别切椭圆C与圆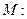
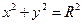 (其中
(其中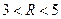 )于
)于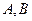 两点,求
两点,求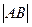 的最大值。
的最大值。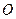 为坐标原点,
为坐标原点,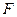 为椭圆
为椭圆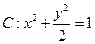 在
在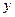 轴正半轴上的焦点,过
轴正半轴上的焦点,过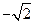 的直线
的直线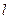 与
与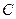 交与
交与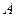 、
、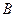 两点,点
两点,点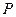 满足
满足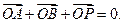
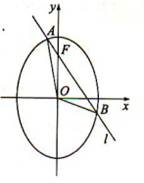
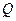 ,证明:
,证明: :
: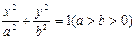 的焦点分别为
的焦点分别为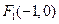 、
、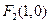 ,抛物线
,抛物线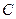 :
: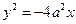 的准线与
的准线与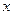 轴的交点为
轴的交点为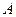 ,且
,且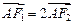 .
.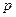 的值及椭圆
的值及椭圆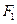 、
、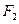 分别作互相垂直的两直线与椭圆分别交于
分别作互相垂直的两直线与椭圆分别交于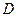 、
、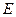 、
、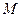 、
、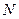 四点(如图),
四点(如图),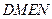 面积的最大值和最小值.
面积的最大值和最小值.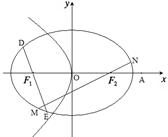
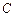 :
: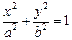 (
(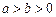 ),其焦距为
),其焦距为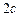 ,若
,若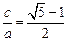 (
(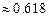 ),则称椭圆
),则称椭圆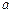 、
、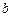 、
、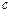 成等比数列.
成等比数列.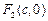 ,
,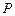 为椭圆
为椭圆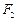 、
、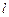 ,使
,使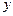 轴的交点
轴的交点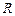 满足
满足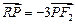 ?若存在,求直线
?若存在,求直线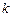 ;若不存在,请说明理由.
;若不存在,请说明理由.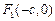 、
、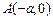 、
、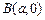 、
、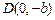 、
、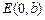 为顶点的菱形
为顶点的菱形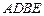 的内切圆过焦点
的内切圆过焦点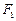 、
、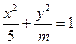 表示是焦点在y轴上的椭圆;q:三次函数
表示是焦点在y轴上的椭圆;q:三次函数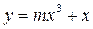
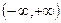 内单调递增,.求使“
内单调递增,.求使“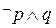 ”为真命题的实数m的取值范围.
”为真命题的实数m的取值范围.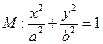
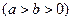 的离心率为
的离心率为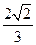 ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为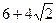 .
.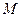 的方程;
的方程;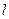 与椭圆
与椭圆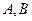 两点,且以
两点,且以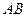 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点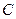 ,
,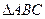 面积的最大值.
面积的最大值.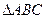 中,∠ABC=450,∠ACB=600,
中,∠ABC=450,∠ACB=600, ,记以AC为母线的圆锥为M2,m是圆锥M1任一母线,则圆锥M2的母线中与m垂直的直线有 ▲ 条
,记以AC为母线的圆锥为M2,m是圆锥M1任一母线,则圆锥M2的母线中与m垂直的直线有 ▲ 条