题目内容
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2a6 .
(1)求数列{an}的通项公式;
(2)设bn=|10+2log3an|,求数列{bn}的前n项和Sn .
【答案】
(1)解:设等比数列{an}的各项均为正数,且公比为q(q>0),
由2a1+3a2=1,a32=9a2a6,可得:
2a1+3qa1=1,(a1q2)2=9a12q6,
解得a1=q= ![]() ,
,
可得数列{an}的通项公式为an=a1qn﹣1=( ![]() )n;
)n;
(2)解:bn=|10+2log3an|=|10+2log33﹣n|=|10﹣2n|,
当1≤n≤5时,bn=10﹣2n,
前n项和Sn= ![]() (8+10﹣2n)n=9n﹣n2;
(8+10﹣2n)n=9n﹣n2;
当n>5时,前n项和Sn=8+6+4+2+0+2+4+6+…+2n﹣10
=20+ ![]() (2+2n﹣10)(n﹣5)=n2﹣9n+40.
(2+2n﹣10)(n﹣5)=n2﹣9n+40.
综上可得,前n项和Sn= ![]() .
.
【解析】(1)设等比数列{an}的各项均为正数,且公比为q(q>0),运用等比数列的通项公式,解方程可得首项和公比为 ![]() ,运用等比数列的通项公式即可得到所求;(2)求得bn=|10+2log3an|=|10+2log33﹣n|=|10﹣2n|,讨论当1≤n≤5时,当n>5时,运用等差数列的求和公式,计算即可得到所求和.
,运用等比数列的通项公式即可得到所求;(2)求得bn=|10+2log3an|=|10+2log33﹣n|=|10﹣2n|,讨论当1≤n≤5时,当n>5时,运用等差数列的求和公式,计算即可得到所求和.
【考点精析】掌握等比数列的通项公式(及其变式)和数列的前n项和是解答本题的根本,需要知道通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系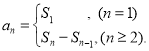 .
.

【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式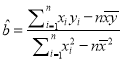 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.