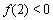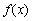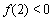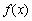题目内容
已知a，b为常数，a≠0，
，适合f (3)=1，且f (x)=x有唯一解．
(1) 当xn=f (xn－1) (n>1)时，数列
是何数列？
(2) 设x1=a，求这个数列前2n+1项中奇数项和与偶数项和的比．
答案：
解析：
解析：
(1) 由f (3)=1，得 ，3a+b=3，
由f (x)=x有唯一解，即 ∴ x=0且b=1，代入3a+b=3，得 ∴ 当xn=f (xn－1) (n>1)时， ∴ 故 (2) ∵ x1=a．∴ 在前2n+1项中，奇数项共n+1项，偶数项共n项，公差为
∴
|
有唯一解，x(ax+b－1)=0有唯一解．
．
．
．
，即
(常数)．
是等差数列．
，又公差
，
．
，
．
．
练习册系列答案
相关题目
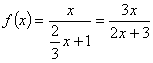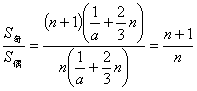(1－a)x2－3ax＋b．
，求a，b的值．
