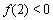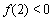题目内容
已知a,b为常数,a≠0,f(x)=ax2+bx,f(2)=0,方程f(x)=x有二个相等的实数解.
(1)求f(x)的解析式.
(2)当x∈[1,2]时,求f(x)值域.
(1)求f(x)的解析式.
(2)当x∈[1,2]时,求f(x)值域.
分析:(1)由f(2)=0,可得 4a+2b=0 ①.由方程 f(x)=x即ax2+(b-1)x=0有二个相等的实数解,且a≠0.可得△=0 ②. 由①、②解得b和a的值,可得 f(x)的解析式.
(2)由(1)知 f(x)=-
(x-1)2+
,再利用二次函数的性质求得当x∈[1,2]时,f(x)的值域.
(2)由(1)知 f(x)=-
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)由f(2)=0,可得 4a+2b=0 ①.
方程 f(x)=x 即 ax2+bx=x,即 ax2+(b-1)x=0有二个相等的实数解,且a≠0.
∴△=(b-1)2-4a=0 ②.
由①、②解得 b=1,a=-
,
∴f(x)=-
x2+x.
(2)由(1)知 f(x)=-
x2+x=-
(x-1)2+
,
对称轴x=1开口向下,在[1,2]上是减函数,故当x=1时,y=
为最大值; 当x=2时,y=0为最小值.
故当x∈[1,2]时,f(x)的值域为[0,
].
方程 f(x)=x 即 ax2+bx=x,即 ax2+(b-1)x=0有二个相等的实数解,且a≠0.
∴△=(b-1)2-4a=0 ②.
由①、②解得 b=1,a=-
| 1 |
| 2 |
∴f(x)=-
| 1 |
| 2 |
(2)由(1)知 f(x)=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
对称轴x=1开口向下,在[1,2]上是减函数,故当x=1时,y=
| 1 |
| 2 |
故当x∈[1,2]时,f(x)的值域为[0,
| 1 |
| 2 |
点评:本题主要考查函数的零点与方程的根的关系,利用二次函数的性质求函数的值域,属于中档题.

练习册系列答案
相关题目