题目内容
【题目】已知递增等比数列{an},满足a1=1,且a2a4﹣2a3a5+a4a6=36.
(1)求数列{an}的通项公式;
(2)设bn=log3an+ ![]() ,求数列{an2bn}的前n项和Sn;
,求数列{an2bn}的前n项和Sn;
(3)在(2)的条件下,令cn= ![]() ,{cn}的前n项和为Tn , 若Tn>λ恒成立,求λ的取值范围.
,{cn}的前n项和为Tn , 若Tn>λ恒成立,求λ的取值范围.
【答案】
(1)解:设递增等比数列{an}的公比为q,
由等比数列的性质可得,a32﹣2a3a5+a52=36,
即有(a3﹣a5)2=62,
可得a5﹣a3=6,
即q4﹣q2=6,解得q2=3(﹣2舍去),
即有q= ![]() ,数列{an}的通项公式为an=(
,数列{an}的通项公式为an=( ![]() )n﹣1
)n﹣1
(2)解:bn=log3an+ ![]() =(n﹣1)log3
=(n﹣1)log3 ![]() +
+ ![]() =
= ![]() ,
,
数列{an2bn}的通项为 ![]() n3n﹣1.
n3n﹣1.
前n项和Sn= ![]() (1+23+332+433+…+n3n﹣1),
(1+23+332+433+…+n3n﹣1),
3Sn= ![]() (13+232+333+434+…+n3n),
(13+232+333+434+…+n3n),
两式相减可得,﹣2Sn= ![]() (1+3+32+33+…+3n﹣1﹣n3n)
(1+3+32+33+…+3n﹣1﹣n3n)
= ![]() (
( ![]() ﹣n3n),化简可得Sn=
﹣n3n),化简可得Sn= ![]() ﹣
﹣ ![]()
(3)解:cn= ![]() =
= ![]() =4(
=4( ![]() ﹣
﹣ ![]() ),
),
{cn}的前n项和为Tn=4( ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )
)
=4( ![]() ﹣
﹣ ![]() )=2﹣
)=2﹣ ![]() ,
,
由2﹣ ![]() 为递增数列,即有n=1时,取得最小值2﹣
为递增数列,即有n=1时,取得最小值2﹣ ![]() =
= ![]() .
.
由Tn>λ恒成立,可得λ< ![]()
【解析】(1)设递增等比数列{an}的公比为q,由等比数列的通项和性质,计算即可得到q,进而得到通项公式;(2)化简bn=log3an+ ![]() =(n﹣1)log3
=(n﹣1)log3 ![]() +
+ ![]() =
= ![]() ,再由数列的求和方法:错位相减法可得前n项和Sn;(3)求得cn=
,再由数列的求和方法:错位相减法可得前n项和Sn;(3)求得cn= ![]() =
= ![]() =4(
=4( ![]() ﹣
﹣ ![]() ),运用裂项相消求和,可得Tn , 判断单调性,求得最小值,再由不等式恒成立思想可得λ的取值范围.
),运用裂项相消求和,可得Tn , 判断单调性,求得最小值,再由不等式恒成立思想可得λ的取值范围.
【考点精析】解答此题的关键在于理解等比数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() ,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系
,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系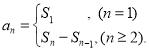 .
.

【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x与相应的生产能耗y的几组对照数据
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() .(其中
.(其中 ,
, ![]() ).
).