题目内容
已知函数f(x)=2mx2-2(4-m)x+1,g(x)=mx,若对于任一实数x,f(x)与g(x)至少有一个为正数,则实数m的取值范围是( )
| A.(0,2) | B.(0,8) | C.(2,8) | D.(-∞,0) |
B
当m≤0时,显然不成立,当m>0时,因f(0)=1>0,当- =
= ≥0即0<m≤4时结论显然成立;
≥0即0<m≤4时结论显然成立;
当- =
= <0时只要Δ=4(4-m)2-8m=4(m-8)(m-2)<0,即4<m<8,则实数m的取值范围是0<m<8,故选B.
<0时只要Δ=4(4-m)2-8m=4(m-8)(m-2)<0,即4<m<8,则实数m的取值范围是0<m<8,故选B.
 =
= ≥0即0<m≤4时结论显然成立;
≥0即0<m≤4时结论显然成立;当-
 =
= <0时只要Δ=4(4-m)2-8m=4(m-8)(m-2)<0,即4<m<8,则实数m的取值范围是0<m<8,故选B.
<0时只要Δ=4(4-m)2-8m=4(m-8)(m-2)<0,即4<m<8,则实数m的取值范围是0<m<8,故选B.
练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目

 ,求
,求 的最大值与最小值;
的最大值与最小值;  的最大值与最小值;
的最大值与最小值; 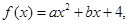 集合
集合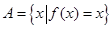
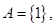 求函数
求函数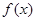 的解析式;
的解析式;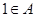 ,且
,且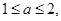 设
设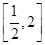 上的最大值、最小值分别为
上的最大值、最小值分别为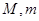 ,记
,记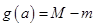 ,求
,求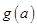 的最小值.
的最小值. 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,椭圆上异于长轴顶点的任意点
,椭圆上异于长轴顶点的任意点 与左右两焦点
与左右两焦点 、
、 构成的三角形中面积的最大值为
构成的三角形中面积的最大值为 .
. ,连接
,连接 与椭圆的另一交点记为
与椭圆的另一交点记为 ,若
,若 与椭圆的另一交点记为
与椭圆的另一交点记为 ,求
,求 的取值范围.
的取值范围. .设
.设 ,
, (max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记
(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记 的最小值为A,
的最小值为A, 的最大值为B,则
的最大值为B,则 ( )
( )


 恒成立,则实数x的值为 .
恒成立,则实数x的值为 . ,例如:
,例如: ,
,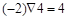 ,则函数
,则函数 的最大值为____________.
的最大值为____________.