题目内容
(13分)如图，四棱锥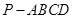
的底面是正方形，
，点
在棱
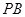上.
（Ⅰ）求证：平面
；
（Ⅱ）当
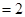且为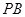的中点时,求四面体
体积.
（Ⅰ）见解析；（Ⅱ）四面体体积为
。
解析
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
同步轻松练习系列答案课课通课程标准思维方法与能力训练系列答案题目内容
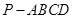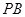(13分)如图，四棱锥的底面是正方形，，点在棱上.
（Ⅰ）求证：平面；
（Ⅱ）当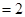且为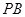的中点时,求四面体体积.
（Ⅰ）见解析；（Ⅱ）四面体体积为。
解析
同步轻松练习系列答案课课通课程标准思维方法与能力训练系列答案
中，底面
是矩形，
，
、
分别为线段
、
的中点，
⊥底面
∥平面
；
^平面
；
，求三棱锥
的体积. 
中,
⊥平面
，
，
,
,
,
是
的中点.
；
与平面
，
，E为棱
的中点．
； (Ⅱ) 求证：
平面
；
的体积．
如图所示，其中
,
,
，求直角梯形以BC为旋转轴旋转一周形成的几何体的表面积。
中，底面
是边长为
的正方形，
为
与
的交点，
，
是线段
的中点．
平面
；
的体积
的棱AP、AB上的点，且AD:DP=AE:EB=1:3.求证：DE//平面PBC