题目内容
已知抛物线C: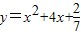 ,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.(Ⅰ)若C在点M的法线的斜率为-
 ,求点M的坐标(x,y);
,求点M的坐标(x,y);(Ⅱ)设P(-2,a)为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P?若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由.
【答案】分析:(1)由切线和法线垂直,则其斜率之积等于-1,可得M处的切线的斜率k=2,再根据导数的几何意义,结合已知即可求得点M的坐标;
(2)设M(x,y)为C上一点,分x=-2和x≠-2两种情况讨论,结合题意和导数的几何意义可得到等量关系(x+2)2=a,然后再分a>0,a=0,a<0三种情况分析,即可求解.
解答:解:(Ⅰ)由题意知,M处的切线的斜率k=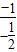 =2,
=2,
∵y′=2x+4,
∴2x+4=2,解得x=-1,
将x=-1代入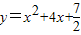 中,解得y=
中,解得y= ,
,
∴M(-1, );
);
(Ⅱ)设 M(x,y)为C上一点,
①若x=-2,则C上点M(-2,- )处的切线斜率 k=0,过点M(-2,-
)处的切线斜率 k=0,过点M(-2,- ) 的法线方程为x=-2,此法线过点P(-2,a);
) 的法线方程为x=-2,此法线过点P(-2,a);
②若 x≠-2,则过点 M(x,y)的法线方程为:y-y=-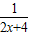 (x-x) ①
(x-x) ①
若法线过P(-2,a),则 a-y=-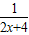 (-2-x),即(x+2)2=a ②
(-2-x),即(x+2)2=a ②
若a>0,则x=-2±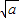 ,从而y=
,从而y=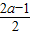 ,将上式代入①,
,将上式代入①,
化简得:x+2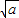 y+2-2a
y+2-2a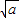 =0或x-2
=0或x-2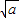 y+2+2a
y+2+2a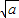 =0,
=0,
若a=0与x≠-2矛盾,若a<0,则②式无解.
综上,当a>0时,在C上有三个点(-2+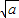 ,
,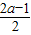 ),(-2-
),(-2-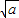 ,
,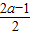 )及
)及
(-2,- ),在这三点的法线过点P(-2,a),其方程分别为:
),在这三点的法线过点P(-2,a),其方程分别为:
x+2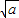 y+2-2a
y+2-2a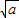 =0,x-2
=0,x-2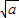 y+2+2a
y+2+2a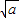 =0,x=-2.
=0,x=-2.
当a≤0时,在C上有一个点(-2,- ),在这点的法线过点P(-2,a),其方程为:x=-2.
),在这点的法线过点P(-2,a),其方程为:x=-2.
点评:本题通过曲线的切线和法线问题,考查了导数的运算和几何意义,同时综合运用了分类讨论的数学思想,难度较大.
(2)设M(x,y)为C上一点,分x=-2和x≠-2两种情况讨论,结合题意和导数的几何意义可得到等量关系(x+2)2=a,然后再分a>0,a=0,a<0三种情况分析,即可求解.
解答:解:(Ⅰ)由题意知,M处的切线的斜率k=
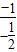 =2,
=2,∵y′=2x+4,
∴2x+4=2,解得x=-1,
将x=-1代入
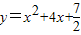 中,解得y=
中,解得y= ,
,∴M(-1,
 );
);(Ⅱ)设 M(x,y)为C上一点,
①若x=-2,则C上点M(-2,-
 )处的切线斜率 k=0,过点M(-2,-
)处的切线斜率 k=0,过点M(-2,- ) 的法线方程为x=-2,此法线过点P(-2,a);
) 的法线方程为x=-2,此法线过点P(-2,a);②若 x≠-2,则过点 M(x,y)的法线方程为:y-y=-
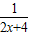 (x-x) ①
(x-x) ①若法线过P(-2,a),则 a-y=-
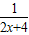 (-2-x),即(x+2)2=a ②
(-2-x),即(x+2)2=a ②若a>0,则x=-2±
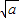 ,从而y=
,从而y=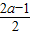 ,将上式代入①,
,将上式代入①,化简得:x+2
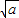 y+2-2a
y+2-2a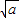 =0或x-2
=0或x-2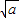 y+2+2a
y+2+2a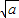 =0,
=0,若a=0与x≠-2矛盾,若a<0,则②式无解.
综上,当a>0时,在C上有三个点(-2+
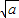 ,
,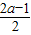 ),(-2-
),(-2-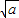 ,
,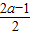 )及
)及(-2,-
 ),在这三点的法线过点P(-2,a),其方程分别为:
),在这三点的法线过点P(-2,a),其方程分别为:x+2
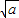 y+2-2a
y+2-2a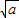 =0,x-2
=0,x-2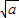 y+2+2a
y+2+2a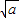 =0,x=-2.
=0,x=-2.当a≤0时,在C上有一个点(-2,-
 ),在这点的法线过点P(-2,a),其方程为:x=-2.
),在这点的法线过点P(-2,a),其方程为:x=-2.点评:本题通过曲线的切线和法线问题,考查了导数的运算和几何意义,同时综合运用了分类讨论的数学思想,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
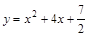 ,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.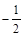 ,求点M的坐标(x0,y0);
,求点M的坐标(x0,y0);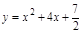 ,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.若C在点M的法线的斜率为
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.若C在点M的法线的斜率为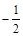 ,求点M的坐标(x0,y0)
,求点M的坐标(x0,y0)