题目内容
已知抛物线C: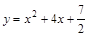 ,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
(1)若C在点M的法线的斜率为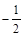 ,求点M的坐标(x0,y0);
,求点M的坐标(x0,y0);
(2)设P(-2,a)为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P?若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由.
【答案】
M(-1,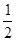 )(2)当a>0时,有三个点(-2+
)(2)当a>0时,有三个点(-2+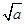 ,
,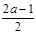 ),(-2-
),(-2-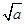 ,
,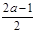 )及(-2,-
)及(-2,-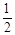 );法线过点P(-2,a),其方程分别为:
);法线过点P(-2,a),其方程分别为:
x+2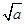 y+2-2a
y+2-2a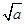 =0,x-2
=0,x-2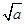 y+2+2a
y+2+2a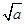 =0,x=-2;
=0,x=-2;
a≤0时,有一个点(-2,-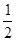 )法线过点P(-2,a),其方程为:x=-2。
)法线过点P(-2,a),其方程为:x=-2。
【解析】(1)由题意设过点M的切线方程为: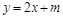 ,代入C得
,代入C得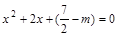 ,
,
则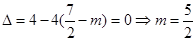 ,∴
,∴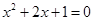

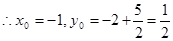 ,
,
即M(-1,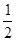 ).
).
(2)当a>0时,假设在C上存在点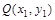 满足条件.设过Q的切线方程为:
满足条件.设过Q的切线方程为: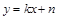 ,代入
,代入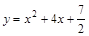
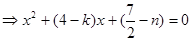 ,则
,则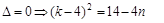 ,
,
且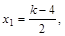
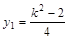 .当
.当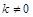 时,由于
时,由于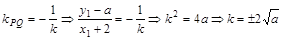 ,
,
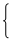
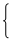 ∴
∴ 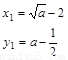 或
或  ;当k=0时,显然
;当k=0时,显然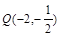 也满足要求.
也满足要求.
∴有三个点(-2+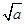 ,
,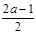 ),(-2-
),(-2-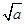 ,
,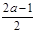 )及(-2,-
)及(-2,-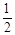 ),
),
且过这三点的法线过点P(-2,a),其方程分别为:
x+2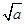 y+2-2a
y+2-2a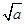 =0,x-2
=0,x-2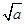 y+2+2a
y+2+2a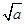 =0,x=-2.
=0,x=-2.
当a≤0时,在C上有一个点(-2,-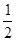 ),在这点的法线过点P(-2,a),其方程为:x=-2.
),在这点的法线过点P(-2,a),其方程为:x=-2.
考点:抛物线与直线相切。
点评:在解决抛物线与直线相切的问题时,一般联立直线方程与抛物线方程,得关于x的一元二次方程,然后利用方程有唯一解,△=0来求解。

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
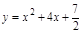 ,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.若C在点M的法线的斜率为
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.若C在点M的法线的斜率为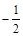 ,求点M的坐标(x0,y0)
,求点M的坐标(x0,y0)