Question

【题目】已知p：指数函数f(x)＝(2a－6)x在R上是单调减函数；q：关于x的方程x2－3ax＋2a2＋1＝0的两根均大于3，若p或q为真，p且q为假，求实数a的取值范围．

Answer 1

【答案】(，3]∪[，＋∞).

【解析】试题分析：根据指数函数的单调性求出命题p为真命题时a的范围，利用二次方程的实根分布求出命题q为真命题时a的范围；
据复合命题的真假与构成其简单命题真假的关系将“p或q为真，p且q为假”转化为p ，q的真假，列出不等式解得．

试题解析：

p真，则指数函数f(x)＝(2a－6)x的底数2a－6满足0<2a－6<1，所以3<a<.

q真，令g(x)＝x2－3ax＋2a2＋1，易知其为开口向上的二次函数．因为x2－3ax＋2a2＋1＝0的两根均大于3，所以①Δ＝(－3a)2－4(2a2＋1)＝a2－4>0，a<－2或a>2；②对称轴x＝－＝>3；③g(3)>0，即32－9a＋2a2＋1＝2a2－9a＋10>0，所以(a－2)(2a－5)>0.所以a<2或a>.

由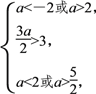得a>.

p真q假，由3<a<及a≤，得a∈.

p假q真，由a≤3或a≥及a>，得<a≤3或a≥.

综上所述，实数a的取值范围为(，3]∪[，＋∞).